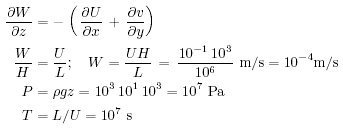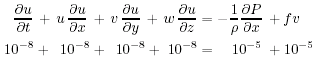Capitolo10 - Le Correnti Geostrofiche

10.1 L'Equilibrio Idrostatico

All'interno dell'oceano lontano dallo strato di Eckman di superfice e del fondo, per distanze orizzontali più grandi di poche decine di kilometri, e per tempi più grandi di pochi giorni, i gradienti orizzontali di pressione nell'Oceano, bilanciano quasi esattamente la forza di Coriolis, risultante dalle correnti orizzontali. Questo bilancio é conosciuto come il bilancio geostrofico.

Le forze dominanti che agiscono nella verticale sono il gradiente verticale di pressione ed il peso dell'acqua. I due termini si bilanciano entro poche parti per milione. Così la pressione ad ogni punto della colonna d'acqua é dovuta quasi interamente al peso dell'acqua nella colonna sopra il punto. Le forze dominanti nell'orizzontale sono il gradiente di pressione e la forza di Coriolis. Si bilanciano entro poche parti per milione su grandi distanze e tempi lunghi (vedi il riquadro).

Scalando le Equazioni: L'Approssimazione Geostrofica

Vogliamo semplificare le equazioni del moto per ottenere le soluzioni che descrivono le condizioni del mare profondo, ben lontano dalle coste e sotto lo strato limite di Echman superficiale. Per cominciare, esaminiamo la grandezza tipica di ogni termine delle equazioni, nella speranza che alcuni sono così piccoli che possono essere tolti senza canbiare le caratteristche dominanti della soluzione. Per le condizioni interne di un mare profondo, valori tipici della distanza L, velocità orizzontale U, profondità H, parametro di Coriolis f, gravità g, e densità r sono: L » 106m f» 10-4s-1 U» 10-1m/s g» 10 m/s2 H» 103m r » 103kg/m3 Da queste variabili possiamo calcolare i tipici valori per la velocità verticale W, pressione P, e tempo T: L'equazione del momento per velocità verticale é quindi: ed il solo bilancio importante nella verticale é quello idrostatico: L'equazione del momento per la velocità orizzontale nella direzione x é: Così la forza di Coriolis balancia quella del gradiente di pressione dentro una parte per mille. Questo é detto il bilancio geostrofico, e le equazioni geostrofiche sono: Questo bilancio si applica a flussi oceanici con dimensioni orizzontali più grandi di circa 50 km e tempi più lunghi di pochi giorni.

Entrambi i bilanci richiedono che la viscosità ed i termini non lineari nelle equazioni del moto siano trascurabili. Questo é ragionevole? Consideriamo la viscosità. Noi sappiamo che una barca a remi di un centinaio di chili può andare per decine di metri dopo che il rematore si ferma. Una superpetroliera che si muove con la velocità della barca a remi può navigare per centinaia di metri. Sembra ragionevole, quindi, che un kilometro cubo di acqua che pesa 10¹⁵kg dovrebbe andare per forse un giorno prima di fermarsi lentamente. Un vortice oceanico di mesoscala contiene forse 1000 kilometri cubi di acqua. Quindi, la nostra intuizione può portarci a colcludere che trascurare la viscosità é ragionevole. Naturalmente, l'intuizione può essere sbagliata, e abbiamo bisogno di tornare indietro per ripesare gli argomenti.

10.1 L'Equilibrio Idrostatico
Prima di descrivere il bilancio geostrofico, consideriamo prima la soluzione più semplice dell'equazione del momento, la soluzione per un oceano fermo. Ci fornisce la pressione idrostatica dentro l'Oceano. Per ottenere la soluzione, assumiamo che il fluido sia fermo, non é in movimento:

il fluido rimane fermo:

(10.2)

e, che non ci sia attrito:

Con queste assunzioni le quazioni del momento (7.12) diventano:

(10.4)

dove abbiamo espicitamente scritto che la gravità g é una funzione della latitudine φ e dell'altezza z. Mostreremo più tardi perché abbiamo tenuto questo in chiaro.

Le equazioni (10.4a) richiedono che le superfici di pressione constante siano superfici di livello. Una superfice di pressione costante é una superfice isobarica. L'ultima equazione può essere integrata per ottenere la pressione ad ogni profondità h. Ricordiamo che r é una funzione della profondità per un oceano fermo.

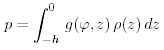(10.5)

Per molti scopi, g e ρ sono constanti, e p = g h ρ . Più in là , mostreremo che la (10.5) si applica con una accuratezza di circa una parte per milione anche se l'oceano non é fermo.

L'unità di misura SI per la pressione é il pascal (Pa). Il bar é un'altra unità della pressione. Un bar é esattamente10⁵ Pa (Tabella 10.1). Poiché la profondità in metri e la pressione in decibar numericamente sono quasi le stesse, gli oceanografi preferiscono specificare la pressione in decibar.

10.2 Le Equazioni Geostrofiche

Il bilancio geostrofico richiede che la forza di Coriolis bilanci i gradienti di pressione orizzontali. Le equazioni per il bilancio geostrofico sono derivate dalle equazioni del moto assumendo che il flusso non abbia accelerazioni, du/dt = dv/dt = dw/dt = 0; che le velocità orizzontali sono molto più grandi di quelle verticali, w << u, v; che la sola forza esterna é la gravità; e che l'attrito é trascurabile. Con queste assunzioni la (7.12) diventa

(10.6)

dove f = 2 Ω sin φ é il parametro di Coriolis. Queste sono le equazioni geostrofiche.

Le equazioni possono essere scritte:

	(10.7a)
	(10.7b)

dove p₀ é la pressione atmosferica a z = 0, e ζ é l'altezza della superfice del mare. Da notare che abbiamo permesso alla superfice del mare di essere sopra o sotto la superfice z = 0; ed il gradiente di pressione alla superfice del mare é bilanciato dalla corrente di superfice u_s.

Sostituendo la (10.7b) dentro la (10.7a) troviamo:

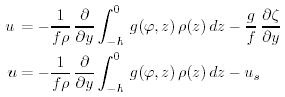	(10.8a)

dove abbiamo usato l'approssimazione di Boussinesq, conservando la piena accuratezza per ρ soltanto quando si calcola la pressione.

In modo simile , possiamo derivare l'equazione per la v.

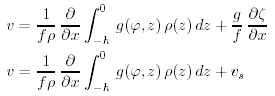	(10.8b)

Se l'oceano é omogeneo e la densità e la gravità sono costanti, il primo termine del lato destro della (10.8) é uguale a zero; e i gradienti di pressione orizzontale dentro l'oceano sono gli stessi come quelli a z = 0. Questo é il flusso barotropico descritto nella §10.4.

Se l'oceano é stratificato, il gradiente di pressione orizzontale ha due termini, uno dovuto alla pendenza della superfice marina, ed un termine addizionale dovuto alle differenze orizzontali della densità. Queste equazioni includono il flusso baroclino discusso anche nel §10.4. Il primo termine sul lato destro dell (10.8) é dovuto a variazioni nella densità ρ(z), ed é chiamato velocità relativa. In tal modo il calcolo delle correnti geostrofiche dalla distribuzione della densità richiede di conoscere la velocità (u₀, v₀) alla superfice del mare o a qualche altra profondità.

10.3 Le Correnti Geostrofiche superficiali dall'Altimetria

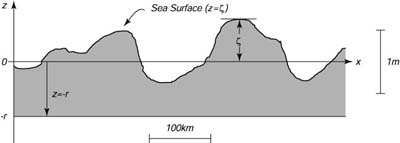
L'approssimazione geostrofica applicata a z = 0, porta ad una relazione molto semplice: le correnti geostrofiche superficiali sono proporzionali alla pendenza della superfice. Consideriamo una superfice di livello leggermente sotto la superfice marina diciamo di due metri, a z = -r. Una superfice di livello é una superfice di potenziale gravitazionale costante, e nessun lavoro é richiesto per muoversi lungo una superfice di livello senza attrito (Figure 10.1).

Figura 10.1 Schizzo che definisce z e r, usati per calcolare la pressione proprio sotto la superfice marina.

La pressione alla superfice di livello é:

assumendo che ρ e g sono essenzialmente constanti nei pochi metri della parte alta dell'oceano. Sostituendo questo dentro la (10.7a, b), abbiamo le due componenti (u_s, v_s) della corrente geostrofica superficiale:

(10.10)

dove g é la gravità, f é il parametro di Coriolis, e ζ é l'altezza della superfice marina sopra il livello superficiale.

La Topografia Oceanica
In §3.4 definiamo la topografia della superfice marina ζ essere l'altezza della superfice del mare relativa ad un particolare livello di superfice, il geoide; e definiamo il geoide essere la superfice di livello che coincide con la superfice dell'oceano fermo. Quindi, in accordo alla (10.10) le correnti geostrofiche superficiali sono proporzionali alla pendenza della topografia (Figure 10.2), una quantità che può essere misurata dal satellite altimetrico se il geoide é conosciuto.

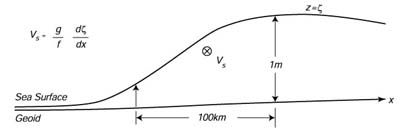
Figura 10.2 La pendenza della superfice marina relativa al geoide (∂z/∂x) é direttamente legata alle correnti geostrofiche di superfice vs. La pendenza di 1 metro per 100 kilometri (10-6 rad) é tipico di correnti forti. Vs ?? is into the paper in the northern hemisphere. ??

Poiché il geoide é una superfice di livello, é una superfice di geopotenziale costante. Per vedere questo, consideriamo il lavoro fatto nel muovere una massa m per una distanza h perpendicolare alla superfice di livello. Il lavoro é W = mgh, ed il cambio di energia potenziale per unità di massa é gh. Così i livelli di superfice sono superfici di geopotenziale costante dove il geopotenziale Φ = gh.

La topografia é dovuta ai processi che causano il movimento dell'oceano: maree, correnti, e il cambio della pressione barometrica che produce l'effetto del barometro invertito. Poiché la topografia del mare é dovuta ai processi dinamici, é generalmente chiamata topografia dinamica. La topografia é approssimativamente un centesimo dell'ondulazione del geoide. Questo significa che la forma della superfice marina é dominata dalle variazioni locali della gravità. L'influenza delle correnti é molto piccola. Tipicamente, la topografia ha un ampiezza di ±1 m. Le pendenze tipiche sono ∂z/∂x ≈ 1-10 microradians for v = 0.1 – 1.0 m/s a latitudini medie.

L'altezza del geoide, lisciata su grandi distanze orizzontali più grandi di circa 400 km, é conosciuta con una accuratezza di ±1 mm dai dati raccolti dalla missione del satellite GRACE (Gravity Recovery and Climate Experiment).

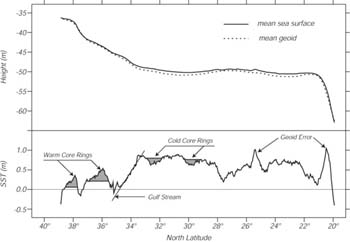
Figura 10.3 Osservazioni dell'altimetro Topex/Poseidon della Corrente del Golfo. Quando le osservanzioni dell'altimetro sono sottratte dal geoide locale, danno la topografia del mare che, in questo esempio, é principalmente dovuta alle correnti marine. Il geoide gravimetrico fu determinato dalla Ohio State University da navi ed altre indagini sulla gravità nella regione. Dal Centro per la Ricerca Spaziale, University of Texas.

Altimetria Satellitare
Sistemi di altimetria satellitare molto accurati sono necessari per misurare la topografia dell'oceano. I primi sistemi, portati su Seasat, Geosat, ERS-1, ed ERS-2 erano progettati per misurare variabilità delle correnti settimana per settimana. Topex/Poseidon, launciato nel1992, fu il primo satellite progettato per fare le misure molto più accurate del necessario per osservare la circolazione superficiale permanente (mediata nel tempo) degli oceani, le maree e la variabilità delle correnti a scala di gyre.

Poiché il geoide non era ben conosciuto localmente prima del 2004, gli altimetri erano fatti volare esattamente per ripetere le stesse tracce. Così il Topex/Poseidon e Jason volano sopra le stesse tracce ogni 9.9156 giorni. Sottrendo l'altezza della superfice del mare da una traccia a quella misurata prima, i cambiamenti della topografia si potevano osservare senza conoscere il geoide. Il geoide é costante nel tempo, e la sottrazione lo rimuove, rivelando solo i cambiamenti dovuti alle correnti, come la variabilità di mesoscala, assumendo che le maree sono state rimosse dai dati (Figure 10.4). La variabilità di Mesoscala include i vortici con un diametro tra circa i 20 km e i 500 km.

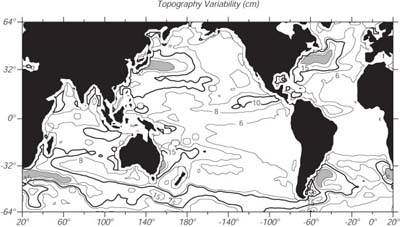
Figura 10.4 Mappa globale della variabilità della topografia dai dati di altimetria satellitare del Topex/Poseidon e dell'ERS dal 12/92 al 11/98. La varianza della topografia é un indicatore della variabilità delle correnti. Da AVISO.

La grande precisione dei sistemi altimetrici del Topex/Poseidon e di Jason permette di misurare la topografia sopra i bacini oceanici con una accuratezza di ±5 cm. Questo permette loro di misurare:

1. I cambiamenti nel volume medio dell'Oceano (Born et al., 1986, Nerem, 1995);
2. Il riscaldamento ed il raffreddamento stagionale dell'Oceano (Chambers et al., 1998);
3. Le maree (Andersen, Woodworth, and Flather, 1995);
4. Il sistema di correnti geostrofiche permanenti della superfice (Figure 10.5);
5. I cambiamenti delle correnti geostrofiche di superfice a tutte le scale (Figure 10.4); e
6. Le variazioni nella topografia del sistema di correnti equatoriali come quelle associate al El Niño (Figure 10.6).

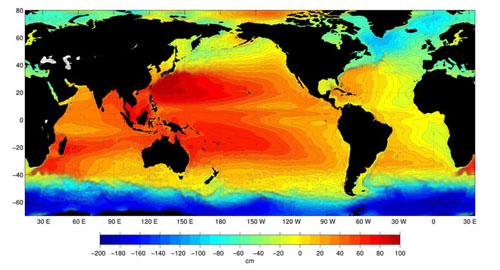
Figura 10.5 Topografia globale, mediata nel tempo, per il periodo 1992–2002 da una analisi congiunta di drifter, altimetri satellitari, vento e GRACE Gravity Model-01 data by Nikolai Maximenko (IPRC) and Peter Niiler (SIO). Le correnti geostrofiche alla superfice del mare sono parallele ai contorni. Compara con la Figura 2.8 calcolata dai dati idrografici. Per maggiori informazioni, vedi Maximenko (2005) (un file pdf da 1MB). Da Asia-Pacific Data-Research Center.

Figura 10.6 traccia tempo-longitudine delle anomalie del livello marino nel Pacifico Equatoriale osservate dal Topex/Poseidon. Le anomalie calde sono in grigio chiaro, quelle fredde sono in grigio scuro. Le anomalie sono calcolate da deviazioni di 10 giorni dalla media superficiale calcolata dal 10/3/1992 al 10/8/1995. I dati sono lisciati con un filtro Gaussiano pesato largo 5° in longitudine e 2° in latitudine. Le annotazioni sulla sinistra sono i cicli dei dati satellitari.

Gli Errori dell'Altimetro (Topex/ Poseidon e Jason)
Le osservazioni più accurate della topografia della superfice marina sono del Topex/Poseidon e Jason. Gli errori per questo sistema di altimetro sono dovuti a :

1. Il rumore degli strumenti, le onde dell'oceano, il vapore acqueo, gli elettroni liberi nella ionosfera, e la massa dell'atmosfera. Topex/Poseidon e Jason portano sistemi altimetrici precisi, capaci di osservare l'altezza del satellite sopra la superfice marina tra ± 66° latitude con una precisione di ±2 cm ed una accuratezza di ±3.2 cm (Fu, et al., 1994). I sistemi consistono di un radar altimetrico a due frequenze per misurare l'altezza dal mare, l'influenza della ionosfera e l'altezza delle onde. I sistemi includono anche un radiometro a micro-onde a tre frequenze capace di misurare il vapore acqueo nella troposfera.
2. Errori di Rotta. I satelliti portano tre sistemi di rotta che abilitano la loro posizione nello spazio, le loro effemeridi, devono essere determinate con una accuratezza di ±3.5 cm (Tapley et al., 1994a).
3. Errori di Campionamento. I satelliti misurano l'altezza lungo una rotta al suolo con un errore inferiore al km che ripetono ogni 9.9156 giorni. Poiché le correnti sono misurate soltanto lungo la rotta del satellite (subsatellite ?) esiste un errore di campionamento. I satelliti non possono mappare la topografia tra le rotte a terra, e nemmeno cambiamenti con periodo minore di 2 x 9.9156 d (vedi §16.3).
4. Errore del Geoide. La topografia permanente non é conosciuta su distanze più corte di poche centinaia di kilometri perché gli errori del geoide dominano per distanze più corte. Le mappe della topografia lisciate su distanzi più grandi, sono usate per studiare le caratteristiche dominanti delle correnti geostrofiche permanenti alla superfice marina (Figure 10.5). I nuovi sistemi dei satelliti GRACE e CHAMP stanno misurando la gravità terrestre con abbastanza accuratezza che presto gli errori del geoide saranno così piccoli da essere ignorati per distanze corte come 100 km.

Presi tutti insieme, le misure dell'altezza dal livello del mare e la posizione del satellite danno le altezze della superfice marina in coordinate geocentriche con una accuratezza di ±4.7 cm. Gli errori del geoide si aggiungono ad altri errori che dipendono dalla grandezza dell'area che deve essere misurata.

10.4 Le Correnti Geostrofiche dall'Idrologia

Le equazioni geostrofiche sono correntemente usate in oceanografia per calcolare le correnti in profondità. L'idea base é di usare le misure idrografiche della temperatura, salinità o conducibilità e pressione per calcolare il campo di densità dell'Oceano usando l'equazione di stato dell'acqua di mare. La densità é usata nella (10.7b) per calcolare il campo di pressione interna, da cui le correnti geostrofiche sono calcolate usando la (10.8a, b). Di solito, comunque, la costante di integrazione della (10.8) non é conosciuta, e soltanto il campo di velocità relativo può essere calcolato.

A questo punto, ci possiamo chiedere, perché non misuriamo direttamente la pressione come si fà in metereologia, dove le misure dirette di pressione sono usate per calcolare i venti? E poi, sono propio necessarie le misure di pressione per calcolare la densità dall'equazione di stato? La risposta é che i cambi molto piccoli nella profondità producono cambi molto grandi in pressione, perché l'acqua é molto più pesante dell'aria. Errori in pressione causati da errori nella determinazione della profondità dallo strumento sono molto più grandi di quelli dovuti alle correnti. Per esempio, usando la (10.7a), calcoliamo che il gradiente di pressione dovuto a 10 cm/s di corrente a 30° di latitudine é 7.5 × 10^-3 Pa/m, che é 750 Pa in 100 km. Dalla equazione idrostatica (10.5), 750 Pa sono equivalenti ad un cambio di profondità di 7.4 cm. Quindi, per questo esempio, dobbiamo sapere la profondità dello strumento con una accuratezza migliore di 7.4 cm. Questo non é possibile.

Le Superfici Geopotenziali Dentro l'Oceano
Il calcolo dei gradienti di pressione dentro l'oceano deve essere fatto lungo le superfici geopotenziali costanti, propio come calcoliamo i gradienti superficiali di pressione relativi al geoide, quando calcoliamo le correnti geostrofiche di superfice. Come quando, nel 1910, Vilhelm Bjerknes comprese che tali superfici non sono ad altezze fisse nell'atmosfera, perché g non é costante, e la (10.4) deve includere la variabilità della gravità in entrambe le direzione orizzontale e verticale (Saunders e Fofonoff, 1976) quando si calcola la pressione nell'oceano.

Il geopotenziale Φ é:

(10.11)

Poiché Φ/9.8 in unità SI ha quasi lo stesso valore numerico dell'altezza in metri, la comunità dei meteorologi accettò la proposta di Bjerknes che l'altezza sia rimpiazzata dai metri dinamici D = Φ/10 per ottenere una coordinata verticale naturale. Più tardi, questa é stata sostituita dal metro geopotenziale (gpm) Z = Φ/9.80. Il metro geopotenziale é la misura del lavoro richiesto per sollevare una unità di massa dal livello del mare ad un altezza z contro la forza di gravità. Harald Sverdrup, uno studente di Bjerknes, portò il concetto in oceanografia, e le profondità dell'oceano sono spesso quotate in metri geopotenziali. La differenza tra profondità di distanza verticale costante e potenziale costante può essere relativamente grande. Per esempio, la profondità geometrica della superfice dei 1000 metri dinamici é di 1017.40 m al polo nord e di 1022.78 m all'equatore, una differenza di 5.38 m.

Da notare che la profondità in metri geopotenziali, in metri, e la profondità in pressione in decibars sono numericamente quasi le stesse. Ad una profondità di 1m la pressione é approssimativamente 1.007 decibars e la profondità e 1.00 metro geopotenziale.

Le Equazioni per le Correnti Geostrofiche nell'Oceano
Per calcolare le correnti geostrofiche, abbiamo bisogno di calcolare il gradiente di pressione orizzontale. Questo può essere fatto usando uno dei due approcci:

1. Calcolare la pendenza di una superfice a pressione costante relativa ad una superfice a geopotenziale costante. Usiamo questo approccio quando usiamo la pendenza della superfice marina dall'altimetria per calcolare le correnti geostrofiche di superfice. La superfice del mare é una superfice a pressione costante. La superfice geopotenziale é il geoide.
2. Calcolare i cambi in pressione su una superfice di geopotenziale costante. Tale superfice é detta superfice geopotenziale.

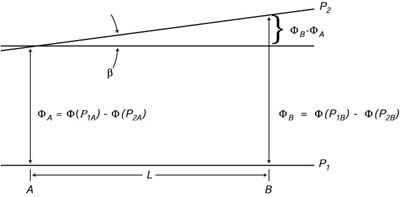
Figura 10.7. Schema della geometria usata per calcolare la corrente geostrofica dai dati idrografici.

Gli oceanografi di solito calcolano la pendenza delle superfici a pressione costante. I passi importanti sono:

1. Calcolare le differenze nel geopotenziale (Φ_A - Φ_B) tra due superfici di pressione constanti (P₁, P₂) alle stazioni idrografiche A e B (Figura 10.7). Questo é simile al calcolo di ζ dello strato superficiale.
2. Calcolare la pendenza della superfice di pressione superiore relativa a quella inferiore.
3. Calcolare la corrente geostrofica at the upper surface relative to the current at the lower. This is the current shear.
4. Integrare lo shear della corrente da un qualche livello dove le correnti sono conosciute per ottenere le correnti in funzione della profondità. Per esempio, dalla superfice verso il basso, usando le correnti geostrofiche di superfice osservate dal satellite altimetrico, oppure verso l'alto assumendo un livello a velocità zero (dove l'acqua é ferma).

Per calcolare le correnti geostrofiche, gli oceanografi usano una forma modificata dell'equazione idrostatica. Il gradiente verticale di pressione della (10.6) é scritto

	(10.12a)
	(10.12b)

dove α = α (S, t, p) é il volume specifico, e la (10.12b) viene dalla (10.11). Differenziando la (10.12b) rispetto alla distanza orizzontale x permette al bilancio geostrofico di essere scritto in termini della pendenza della superfice a pressione costante usando la (10.6) con f = 2Ω sin φ:

	(10.13a)
	(10.13b)

dove Φ é il geopotenziale alla superfice a pressione costante.

Ora guardiamo come i dati idrografici sono usati per valutare ∂ Φ/∂x su una superfice a pressione costante. Integrando la (10.12b) tra due superfici a pressione costante (P₁, P₂) nell'oceano, come mostrato in Figura 10.7 dà la differenza geopotenziale tra due superfici a pressione costante. Alla stazione A, l'integrazione dà :

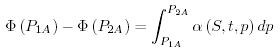(10.14)

L'anomalia del volume specifico é scritta come la somma di due parti:

(10.15)

dove α (35, 0, p) é il volume specifico dell'acqua marina con salinità 35 PSU, temperatura 0° C, e pressione p. Il secondo termine δ é l'anomalia del volume specifico. Usando la (10.15) nella (10.14) otteniamo:

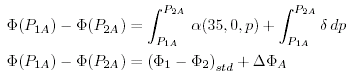dove (Φ₁ - Φ₂)_std é la distanza geopotenziale standard tra due superfici a pressione costante P₁ e P₂, e

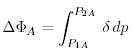(10.16)

é la anomalia della distanza tra le superfici. é chiamata anomalia geopotenziale. La distanza geometrica tra Φ₂ e Φ₁ é numericamente circa ( Φ₂ - Φ₁)/g dove g = 9.8 m/s² é il valore approssimato della gravità. L'anomalia geopotenziale é molto più piccola, essendo circa lo 0.1% della distanza geopotenziale standard.

Consideriamo ora l'anomalia geopotenziale tra due superfici di pressione P₁ e P₂ calcolate a due stazioni idrografiche A e B ad una distanza L metri tra loro (Figure 10.7). Per semplicità assumiamo che la superfice a pressione costante più bassa sia una superfice di livello. Quindi le superfici a pressione costante e geopotenziale coincidono, e non c'é velocità geostrofica a questa profondità. La pendenza della superfice superiore é

poiché la distanza geopotenziale standard é la stessa alla stazione A e B. La velocità geostrofica alla superfice superiore calcolata dalla (10.13b) é:

(10.17)

dove V é la velocità alla superfice geopotenziale superiore. La velocità V é perpendicolare al piano delle due stazioni idrologiche e diretto nel piano della Figura 10.7 se il flusso é nell'emisfero nord. Una utile regola pratica é che il flusso é tale che acqua più calda e leggera é alla destra guardando verso la corrente nell'emisfero nord.

Da notare che, avremmo potuto calcolare la pendenza delle superfici a pressione costante usando la densità ρ invece del volume specifico α. Abbiamo usato quello perché é una pratica comune in oceanografia, e le tabelle delle anomalie del volume specifico ed i programmi di calcolo per valutare le anomalie sono largamente disponibili. La pratica comune deriva dai metodi numerici sviluppati prima che le calcolatrici ed i computer fossero disponibili, quando tutti i calcoli erano fatti a mano o da calcolatrici meccaniche con l'aiuto di tabelle e ?? nomograms?? . Poiché il calcolo deve essere fatto con una accuratezza di poche parti per milione, e poiché tutti i campi scientifici tendono ad essere conservativi, la pratica comune ha continuato ad usare le anomalie del volume specifico piuttosto che le anomalie della densità.

Flusso Barotropico e Flusso Baroclino:
Se l'Oceano fosse omogeneo con densità costante, allora le superfici di pressione costante dovrebbero essere sempre parallele alla superfice marina, e la velocità geostrofica dovrebbe essere indipendente dalla profondità. In questo caso la velocità relativa é zero, ed i dati idrologici non possono essere usati per misurare le correnti geostrofiche. Se la densità varia con la profondità, ma non con la distanza orizzontale, le superfici di pressione costante sono sempre parallele alla superfice del mare ed i livelli di densità costante, le superfici isopicne. Anche in questo caso, il flusso relativo é zero. Entrambi i casi sono esempi di flusso barotropico.

Flusso Barotropico accade quando i livelli di pressione constante nell'Oceano sono sempre paralleli alle superfici di densità constante. Da notare, che alcuni autori chiamano il flusso mediato verticalmente la componente baroclina del flusso. Wunsch (1996: 74) fece notare che il termine baroclinico é usato in molti modi differenti che diventa senza significato e non dovrebbe essere usato.

Flusso Baroclino si manifesta quando i livelli di pressione costante sono inclinati alle superfici di densità costante. In questo caso, la densità varia con la profondità e la posizione orizzontale. Un buon esempio é mostrato in Figure 10.8 dove i livelli di densità costante cambiano profondità per più di un 1km su una distanza orizzontale di 100km nella Corrente del Golfo. Il flusso baroclino varia con la profondità e la corrente relativa può essere calcolata dai dati idrologici. Da notare, le superfici a densità costante non possono essere inclinate alle superfici a pressione costante in un fluido fermo.

In generale, le variazioni verticali del flusso possono essere decomposte in una componente barotropica, che é independente dalla profondità, e una componente baroclina che varia con la profondità.

10.5 Un Esempio usando Dati Idrologici

Consideriamo un calcolo numerico specifico di velocità geostrofiche usando procedure consolidate dal Processing of Oceanographic Station Data (JPOTS Editorial Panel, 1991). Il libro tratta di esempi, usando dati idrografici raccolti dalla R/V Endeavor nel Nord Atlantico. I dati furono prodotti nella crociera 88 lungo 71°W attraverso la Gulf Stream a sud di Capo Cod, Massachusetts dalla stazione 61 alla 64. La stazione 61 é nel Mar dei Sargassi a lato della Gulf Stream in acque profonde 4260m. La stazione 64 é a nord della Gulf Stream con una profondità di 3892m. Le misure furono fatte con una sonda CTD, Mark III CTD/02, della Neil Brown Instruments Systems.

I dati sono campionati 22 volte al secondo, ed i dati digitali erano mediati su intervalli di 2 dbar quando il CTD era calato in acqua. I Dati furono tabulati ad intervalli di 2 dbar centrati sui valori dispari di pressione, perché la prima osservazione é alla superfice, ed il primo intervallo mediato si estende a 2 dbar, ed il centro del primo intervallo é a 1 dbar. I dati furono ulteriormente smussati con un filtro binomiale e linearmente interpolati ai livelli standard riportati nella prima delle tre colonne. Tabella 10.2 e Tabella 10.3. Tutti i trattamenti furono fatti elettronicamente.

δ(S, t, p) nella quinta colonna di Tabella 10.2 e Tabella 10.3 é calcolata dai valori di t, S, p nello strato. <δ> é il valore medio dell'anomalia del volume specifico per lo strato tra i livelli di pressione standard. Esso é la media dei valori di δ(S, t, p) alla cima ed al fondo dello strato. L'ultima colonna (10^-5 ΔΦ) é il prodotto della anomalia media del volume specifico per lo spessore dello strato in decibar. Quindi, l'ultima colonna é l'anomalia geopotenziale ΔΦ calcolata integrando la (10.16) da P₁ al fondo di ogni strato e P₂ alla cima di ogni strato.

La distanza tra le stazioni é L = 110,935 m; Il parametro medio di Coriolis é f = 0.88104 × 10^-4 ed il denominatore nella (10.18) é 0.10231 s/m. Questo fu usato per calcolare le correnti geostrofiche relative a 2000 decibar riportate in Tabella 10.4 e disegnate in Figura 10.8.

Notare che non c'é nessuna indicazione delle correnti di Ekman nella Figura 10.8. Le correnti di Eckman non sono geostrofiche, e non contribuiscono alla topografia. Contribuiscono soltanto indirettamente attraverso la pompa di Ekman (vedi Figura 12.7).

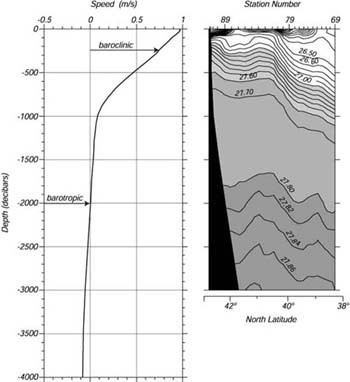
Figura 10.8 Sinistra: Correnti relative, in funzione della profondità, calcolate dai dati idrografici raccolti dalla crociera Endeavor a sud di Cape Cod nell'Agosto 1982. La Gulf Stream é la corrente, più in alto di 1000 decibars più veloce. La profondità di riferimento a velocità zero é stata assunta a 2000 decibar. Destra: Sezione di densità potenziale sq attraverso la Gulf Stream lungo 63.66°W calcolata dai dati di CTD raccolti dalla Endeavor dal 25 al 28 Aprile 1986. La Gulf Stream é centrata sui contorni in ripida pendenza più in alto di 1000m tra 40° and 41°. Notare che la scala verticale é 425 volte quella orizzontale. I dati sono stati elaborati da Lynn Talley, Scripps Institution of Oceanography.

10.6 Commenti sulle Correnti Geostrofiche

Ora che sappiamo come calcolare le correnti geostrofiche dai dati idrologici, consideriamo alcune limitazioni della teoria e della tecnica.

Convertire le Velocità Relative alle Velocità Assolute
I dati idrologici forniscono le correnti geostrofiche relative ad un livello di riferimento. Come possiamo convertire le velocità geostrofiche relative a velocità relative alla Terra?

1. Assumiamo un livello di moto 'no motion': Tradizionalmente, gli oceanografi assumono che ci sia un livello di 'no motion', chiamato anche superfice di riferimento, all'incirca 2,000m sotto la superfice. Questa é l'assunzione usata per derivare le correnti nella Tabella 10.4. Le correnti sono assunte essere uguali a zero a quella profondità, e le correnti relative sono integrate su fino alla superfice e giù fino al fondo per ottenere la velocità della corrente in funzione della profondità. Ci sono evidenze sperimentali che tale livello esiste ?? in media per correnti medie ?? ( on average for mean currents) (vedi per esempio, Defant, 1961: 492).

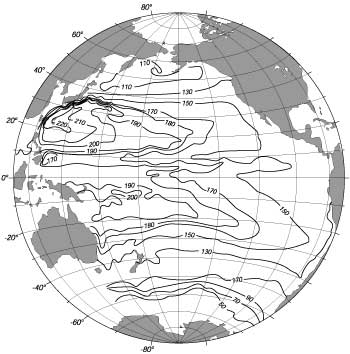
Defant raccomanda di scegliere un livello di riferimento dove lo shear in verticale della corrente sia il più piccolo. Questo di solito é vicino ai 2 km. Ciò porta a mappe utili delle correnti superficiali perché quelle correnti tendono ad essere più veloci di quelle profonde. Figura 10.9 mostra la anomalia geopotenziale e le correnti superficiali del Pacifico relative ad un livello di pressione di 1,000 decibar. Compariamo questo con la Figura 10.5.

Figura 10.9. Mean depth geopotential anomaly ?? dell'Oceano Pacifico relativa alla superfice ai 1,000dbar basata su 36,356 osservazioni. l'altezza é in centimetri geopotenziali. Se la velocità a 1,000dbar fosse zero, la mappa dovrebbe essere la superfice topografica del Pacifico. Da Wyrtki (1974).

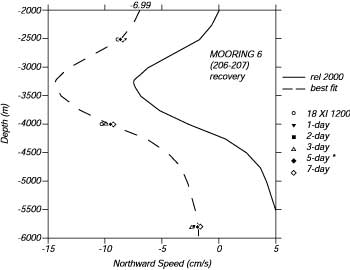
2. Usa correnti conosciute: Le correnti conosciute potrebbero essere misurate da correntometri oppure dai satelliti altimetrici. I problemi sorgono se le correnti non sono state misurate allo stesso tempo dei dati idrologici. Per esempio, i dati idrologici sono stati raccolti in un periodo da mesi a decadi, mentre le correnti possono essere state misurate in un periodo di pochi mesi. Quindi, l'idrologia può non essere consistente con le misure di corrente. Qualche volta le correnti ed i dati idrologici sono stati raccolti quasi nello stesso periodo (Figura 10.10). In questo esempio, le correnti furono misurate continuamente da correntometri ormeggiati (punti) in una western boundary current profonda ed i dati di CTD raccolti poco prima di posizionare i correntometri e dopo il recupero (le curve smussate). La linea piena é la corrente calcolata, assumendo un livello di riferimento a 2,000 m, quella tratteggiata é la corrente aggiustata usando le osservazioni dei correntometri lisciata per i varii intervalli prima e dopo le stazioni CTD.

Figura 10.10 Le misure dei correntometri possono essere usate con le misure CTD per determinare le correnti in funzione della profondità evitando la necessità di assumere una profondità di 'no-motion'. Linea piena: il profilo assume un livello di riferimento a 2000 decibars. Linea tratteggiata: il profilo aggiustato per aderire con le correnti misurate dagli strumenti 1-7 giorni prima delle misure CTD (da Tom Whitworth, Texas A&M University)

3. Uso delle Equazioni di Conservazione: Le linee delle stazioni idrologiche attraverso uno stretto o un bacino possono essere usate insieme alla conservazione della massa e del sale per calcolare le correnti. Questo é l'esempio di un problema inverso (vedi Wunsch, 1996 su come metodi inversi sono usati in oceanografia). Vedi Mercier et al. (2003) per una descrizione di come determinano la circolazione degli strati alti dei bacini orientali dell'Atlantico del sud usando dati idrologici dal World Ocean Circulation Experiment e misure dirette di corrente in un modello a scatole confinato dalla teoria inversa ?????.

Svantaggi nel Calcolare le Correnti dai Dati Idrologici
Le correnti calcolate dai dati idrologici hanno fornito importanti conoscenze della circolazione dell'Oceano nelle decadi dall'inizio del 1900 ad oggi. Tuttavia, é importante passare a vedere i limiti di questa tecnica.

1. I dati idrologici possono essere usati soltanto per calcolare una corrente relativa a quella di un altro livello.
2. L'assunzione di un livello di 'no motion' può essere appropriata in un mare profondo, ma generalmente, non é una utile assunzione quando le acque sono basse come quelle della piattaforma continentale.
3. Le correnti geostrofiche non possono essere calcolate da stazioni idrologiche che sono vicine tra loro. Le stazioni devono stare decine di kilometri lontane.

I Limiti delle Equazioni Geostrofiche
Abbiamo cominciato questa sezione col mostrare che il bilancio geostrofico si applica con buona accuratezza al flusso che si estende a poche decine di kilometri ed a periodi più grandi di pochi giorni. Comunque, il bilancio non può essere perfetto. Se così fosse, il flusso nell'Oceano non dovrebbe mai cambiare perché il bilancio ignora ogni accelerazione del flusso. I limiti più importanti dell'assunzione geostrofica sono:

1. Le correnti geostrofiche non possono evolvere nel tempo peché il bilancio ignora le accelerazioni del flusso. L'accelerazione domina se le dimenisoni orizzontali sono minori di circa 50 km ed i tempi sono minori di pochi giorni. L'accelerazione é trascurabile, ma non zero, su distanze e tempi più lunghi.
2. Il bilancio geostrofico non si applica vicino l'equatore dove la forza di Coriolis diventa zero perché il sin(φ) = 0.
3. Il bilancio geostrofico ignora l'influenza dell'attrito.

Accuratezza
Strub et al. (1997) mostrano che le correnti calcolate dalle misure dei satelliti altimetrici della pendenza superficiale marina hanno un accuratezza di ±3–5 cm/s. Uchida, Imawaki, e Hu (1998) comparano le correnti misurate dai drifter nel Kuroshio con le correnti calcolate dai satelliti altimetrici che misurano le pendenze della superfice marina, assumendo un bilancio geostrofico. Usando le pendenze su distanze superiori a 12.5 km, trovano che le differenze tra le due misure sono ±16 cm/s per correnti fino a 150 cm/s, (circa il 10%). Johns, Watts, e Rossby (1989) misurarono la velocità della Gulf Stream a nord-est di Capo Hatteras e compararono le misure con le velocità calcolate dai dati idrologici assumendo il bilancio geostrofico. Trovarono che la velocità misurata nel centro della corrente, a profondità minori di 500 m, era 10–25 cm/s più grande di quella calcolata dalle equazioni geostrofiche usando misure di velocità a profondità di 2000 m. La velocità massima nel centro era più grande di 150 cm/s, così l'errore era ≈10%. Quando aggiunsero l'influenza della curvatura della Gulf Stream, che aggiunge un termine di accelerazione alle equazioni geostrofico, le differenze nella velocità calcolata ed osservata scendono a meno di 5–10 cm/s (≈5%).

10.7 Le Correnti dalle Sezioni Idrologiche

Le linee dei dati idrologici lungo le rotte della nave sono spesso usate per produrre grafici di contorno della densità lungo la rotta. Le sezioni delle correnti qualche volta mostrano superfici di densita che sprofondano rapidamente con grandi contrasti in densità in entrambi i lati della corrente. Le correnti barocline nella sezione possono essere stimate usando una tecnica proposta per primo da Margules (1906) e descritta da Defant (1961: Capitolo14). La tecnica permette agli oceanografi di stimare la velocità e la direzione della corrente perpendicolare alla sezione da un rapido sguardo alla sezione.

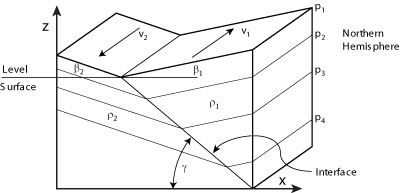
Figura 10.11 Le pendenze β della superfice marina e le pendenze γ dell'interfaccia tra due strati in movimento, omogenei con densità ρ1 e ρ2 nell'emisfero settentrionale. Da Neumann e Pierson (1966).

Per derivare l'equazione di Margules, consideriamo la pendenza ∂z/∂x dell'interfaccia stazionaria tra le due masse d'acqua con densità ρ₁ e ρ₂ (vedi Figura 10.11). Per calcolare il cambio nella velocità attraverso l'interfaccia assumiamo strati omogenei di densità ρ₁ <ρ₂ che sono entrambi in equilibrio geostrofico. Sebbene l'Oceano non ha una interfaccia idealizzata come quella che abbiamo assunto, e le masse di acqua non hanno una densità uniforme, e l'interfaccia tra due masse non é netta, il concetto é ancora utile in pratica.

Il cambio in pressione all'interfaccia é:

(10.18)

ed i gradienti di pressione verticale ed orizzontale sono ottenuti dalla (10.6):

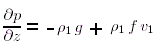(10.19)

Quindi:

	(10.20a)
	(10.20b)

Le condizioni al contorno richiedono δp₁ = δp₂ all'interfaccia se il confine non é in movimento. Eguagliando la (10.20a) con la (10.20b), dividendo per δx, e risolvendo per δz/δx dà:

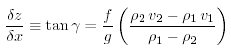	(10.21a)
	(10.21b)
	(10.21c)

dove β é la pendenza della superfice marina, e γ é la pendenza del confine tra le due masse d'acqua. Perché le differenze interne in densità sono piccole, la pendenza é approssimativamente 1000 volte più grande di quella delle superfici pressione costante. Per piccoli valori di β e γ, la β é la pendenza della superfice marina, e la γ é la pendenza dell'interfaccia.

Considera l'applicazione della tecnica alla Gulf Stream (Figura 10.8). Dalla figura: φ = 36°, ρ₁ = 1026.7 kg/m³, e ρ₂ = 1027.5 kg/m³ alla profondità di 500 decibar. Se usiamo la σ_t = 27.1 surface to estimate the slope between the two water masses, we see that the surface changes from a depth of 350 m to a depth of 650 m over a distance of 70 km. Quindi, tan γ = 4300 × 10^-6 = 0.0043, e Δv = v₂ - v₁ = -0.38 m/s. Assumendo v₂ = 0, allora v₁ = 0.38 m/s. Questa é una stima approssimata della velocità della Gulf Stream, che é in buon accordo con la velocità alla profondità di 500 m calcolata dai dati idrologici ( Tabella 10.4) assumendo un livello di 'no motion' a 2,000 decibar.

La pendenza delle superfici a densità costante sono chiaramente visibili nella Figura 10.8. E le figure delle superfici a densità costante possono essere usate rapidamente per stimare le direzioni delle correnti ed un valore approssimato della velocità. In contrast, the slope of the sea surface is 8.4 × 10^-6 or 0.84 m in 100 km se usiamo i dati dalla Table 10.4.

Notare che le superfici a densità costante nella Gulf Stream sprofondano verso est, e la topografia della superfice marina sale verso est. Le superfici a pressione costante e quelle a densità costante hanno pendenze opposite.

Se la ripida interfaccia tra le due masse di acqua raggiunge la superfice, diventa un fronte oceanico. Tali fronti hanno propietà molto simili a quelle dei fronti atmosferici.

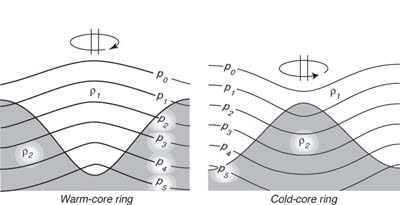
I vortici nelle vicinanze della Gulf Stream possono avere centri caldi o freddi (Figure 10.12). L'applicazione del metodo di Margules a questi vortici fornisce la direzione del flusso. Vortici anticiclonici (rotazione oraria nell'emisfero settentrionale) hanno centri caldi e ρ₁ é più profonda al centro del vortice più che da altre parti) e le superfici a pressione costante si curvano in alto. In particolare, la superfice del mare é più alta al centro. I vortici ciclonici sono al contrario.

Figura 10.12 Mostra la forma delle superfici a pressione costante pi e dell'interfaccia tra due masse d'acqua a densità ρ1, ρ2 se quella superiore sta ruotando più veloce di quella inferiore. Sinistra: Moto Anticiclonico, vortice a centro caldo. Destra: Ciclonico, vortice a centro freddo. La superfice marina p0 pende all'insù verso il centro del vortice a centro caldo, e le superfici a densità costante sprofondano verso il centro. Da Defant (1929).

10.8 Misure di Correnti Lagrangiane

L'Oceanografia e la meccanica dei fluidi distinguono tra due tecniche per la misura delle correnti: Lagrangiana ed Euleriana. Le tecniche Lagrangiane seguono una particella d'acqua. Le tecniche Euleriane misurano la velocità dell'acqua da una posizione fissa.

La Tecnica di Base
Le tecniche lagrangiane tracciano la posizione di un drifter che segue una particella di acqua sia alla superfice che in profondità dentro la colonna d'acqua. La velocità media durante un certo periodo é calcolata dalla distanza tra le posizioni all'inizio ed alla fine del periodo diviso per il periodo. Gli errori sono dovuti a:

1. L'insuccesso del drifter a seguire una porzione d'acqua. Assumiamo che il drifter stia in una porzione di acqua, ma forze esterne che agiscono su di esso possono causare che derivi dalla porzione stessa.
2. Errori nel determinare la posizione del drifter.
3. Errori di campionamento. I drifter vanno soltanto dove i drifter vogliono andare, ed i drifter vogliono andare nelle zone di convergenza. Quindi i drifter tendono ad evitare le aree di flusso divergenti.

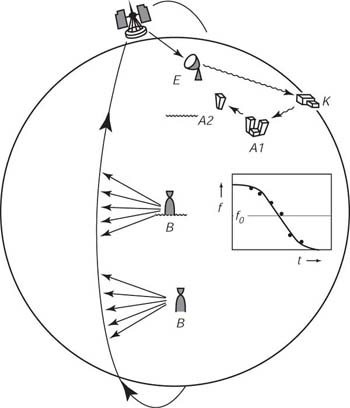
Figure 10.13 I sistemi nei satelliti, specialmente il Sistema Argos, usa segnali radio trasmessi dalle boe per determinare la posizione delle boe stesse. Il satellite S riceve un segnale radio dalla boa B. Il tasso di cambio temporale del segnale, lo spostamento Doppler, é una funzione della posizione della boa e della distanza dalla rotta del satellite. Il segnale Doppler registrato é trasmesso alla stazione a terra E, che comunica l'informazione al centro di calcolo A attraverso la stazione di controllo K. Da Dietrich et al. (1980).

Drifter di Superfice Tracciati dal Satellite
l drifter di superfice consistono di una vela più un galleggiante. La posizione é determinata dal sistema Argos sui satelliti meteorologici (Swenson and Shaw, 1990) o calcolati dai dati GPS registrati in continuo dalla boa e comunicati a terra.

Le boe Argos tracciate portano una radio trasmittente con una frequenza molto stabile F₀. Un ricevitore sul satellite riceve il segnale e determina lo spostamento Doppler F come una funzione del tempo t (Figura 10.13). La frequenza Doppler é

dove R é la distanza della boa, c é la velocità della luce. Più la boa é vicina al satellite, più la frequenza cambia rapidamente. Quando F = F₀ il range é minimo. Questo é il tempo di avvicinamento più prossimo, ed il vettore velocità del satellite é perpendicolare alla linea dal satellite alla boa. Il tempo di avvicinamento più vicino e lo spostamento doppler a quel tempo danno la posizione della boa relativa all'orbita con 180° di ambiguità (B e BB nella figura). Poiché la boa può essere osservata molte volte, la sua posizione può essere determinata senza ambiguità.

La accuratezza della posizione dipende dalla stabilità della frequenza trasmessa dalla boa. I sistemi Argos tracciano le boe con un errore di ±1–2 km, misurando 1–8 posizioni al giorno a seconda dalla latitudine. Poiché 1 cm/s ≈ 1 km/day, e poiché i valori tipici delle correnti in un oceano vanno da 1 a 200 centimetri al secondo, questa é una precisione molto utile.

Drifter Holey-Sock
Il più usato, drifter tracciato dal satellite é quello 'holey-sock'. Consiste di una vela circolare, cilindrico di 1m di diametro lunga 15m con 14 grandi fori tagliati nel cilindro. Il peso della vela é bilanciato da un galleggiante sommerso a 3 m sotto la superfice. Quest'ultimo é collegato ad un gallegiante superficiale parzialmente sommerso che porta il trasmettitore Argos.

La boa fu progettata per il Surface Velocity Program ed é stata provata a lungo. Niiler et al. (1995) misurarono con molta cura la risposta della boa in acqua alle varie velocità del vento, trovarono che la boa si muove 12± 9° alla destra del vento ad una velocità

(10.22)

dove DAR é il rapporto area di drag definito come l'area di attrito della vela diviso per la somma dell'area di attrito del corpo collegato, e D é la differenza in velocità dell'acqua tra la vela cilindrica ed il fondo del mare. Tipicamente i drifter hanno un DAR di 40, e la U_s del drifter < 1 cm/s per U₁₀ < 10m/s.

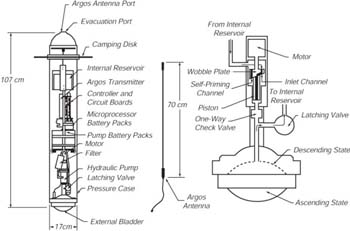
Figura 10.14 I drifter Autonomous Lagrangean Circulation Explorer (ALACE) sono molto usati dal World Ocean Circulation Experiment per misurare le correnti più profonde all'interno dell'Oceano. Sinistra: Schema del drifter. Per salire, la pompa idraulica muove l'oilo dalla riserva interna alla vescica esterna, riducendo la densità del drifter. Per scendere, la valvola si apre per permettere all'olio di tornare indietro nella riserva interna.L'antenna é montata in cima. Destra: Schema ingrandito del sistema idraulico. Il motore ruota il rotore a disco oscillante che muove il pistone che pompa l'olio. Da Davis et al. (1992).

Galleggianti ARGO
The most widely used subsurface floats are the Argo floats. The floats (Figure 10.14) are designed to cycle between the surface and some predetermined depth. Most floats drift for 10 days at a depth of 1 km, sink to 2 km, then rise to the surface. While rising, they profile temperature and salinity as a function of pressure (depth). The float remains on the surface for a few hours, relays data to shore via the Argos system, then it sinks again to 1 km. Each float carries enough power to repeat this cycle for several years. The float thus measures currents at 1 km depth and density distribution in the upper ocean. Three thousand Argo floats are being deployed in all parts of the ocean for the Global Ocean Data Assimilation Experiment GODAE.

Misure Lagrangiane Usando Traccianti Naturali
Il metodo più comune per misurare il flusso nell'Oceano profondo é di tracciare le porzioni di acqua contenenti molecole che non sono normalmente trovate nell'Oceano. Forse il miglior modo per seguire le porzioni d'acqua é quello di marcarle con sostanze non comuni. Grazie alle prove delle bombe atomiche negli anni 50' e al recente aumento esponenziale dei clorofluorocarburi nell'atmosfera, tali traccianti sono stati introdotti nell'Oceano in grande quantità. Vedi §13.4 per una lista di traccianti usati in oceanografia. La distribuzione di molecole traccianti sono usate per dedurre i movimenti dell'acqua. La tecnica é specialmente utile per calcolare la velocità delle masse di acqua profonde mediata su decenni e per calcolare la diffusione vorticosa.

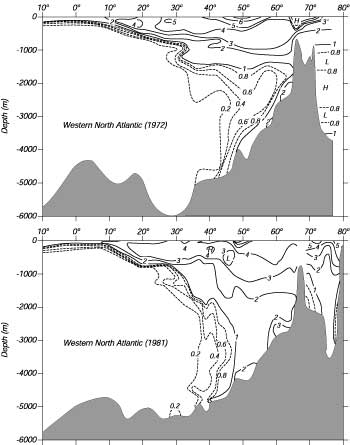
La distribuzione delle molecole traccianti é calcolata dalla concentrazione delle molecole dei campioni raccolti nelle sezioni idrologiche e nelle indagini fatte appositamente. Poiché la collezione dei dati é costosa e lenta, ci sono poche sezioni ripetute. La Figura 10.5 mostra due mappe della distribuzione di trizio nel nord Atlantico, raccolte nel 1972–1973 dal Geosecs Program e nel 1981, una decade più tardi. Le sezioni mostrano che il trizio, introdotto nell'atmosfera durante i test atomici tra il 50 e il 72, é arrivato a profondità sotto i 4 km soltanto a nord del 40°N dal 1971 ed a 35°N dal 1981. Questo mostra che le correnti profonde sono molto lente, circa 1.6 mm/s in questo esempio.

Poiche le correnti profonde sono cosi piccole, possiamo domandarci quali processi sono responsabili delle distribuzioni dei tranccianti osservate. Sia la diffusione turbolenta che l'avvezione dalle correnti non possono essere osservate. Quindi, La Figure 10.15 ci fornisce la corrente media nell'Atlantico profondo, o la diffusione turbolenta del trizio?

Figura 10.15 Distribuzione del trizio lungo una sezione attraverso i bacini occidentali del nord Atlantico, misurata nel 1972 (In Alto) e rimisurata nel 1981 (In Basso). Le unità sono in unità di trizio, dove una unità di trizio é 1018 (atomi di trizio)/(atomi di idrogeno) corretti ai livelli di attività che dovrebbero essere stati osservati il 1 January 1981. Compara questa figura con la densità dell'oceano mostrata in Figura 13.9. Da Toggweiler (1994)

Un altro utile tracciante é la temperatura e la salinità dell'acqua. Considereremo queste osservazioni nel §13.3 dove descriveremo il metodo principale per studiare la circolazione profonda. Qui, notiamo che le osservazioni AVHRR della temperature superficiali dell'Oceano sono una sorgente aggiuntiva delle informazioni sulle correnti.

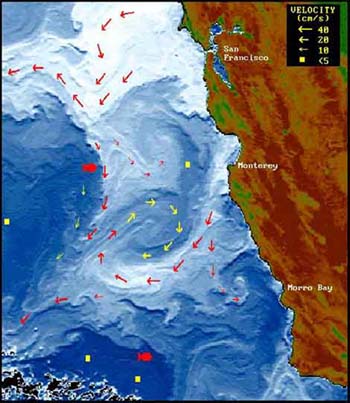
Figura 10.16 Temperatura dell'Oceano e le caratteristiche delle correnti sono combinate in questa analisi AVHRR. Le correnti di superfice sono calcolate tracciando gli spostamenti delle caratteristiche termali e dei sedimenti tra coppie di immagini. Un filtro direzionale ad orlo pronunciato é stato applicato per meglio definire le differenti masse d'acqua. Da Ocean Imaging, Solana Beach, California (con permesso).

Le immagini sequenziali all'infrarosso della temperatura superficiale sono state usate per calcolare gli spostamenti delle caratteristiche delle immagini (Figura 10.16). La tecnica é specialmente utile per controllare la variabilità delle correnti vicino la riva. La terraferma fornisce i punti di riferimento dai quali lo spostamento può essere calcolato con precisione, e grandi differenze di precisione possono essere trovate in molte regioni durante certe stagioni.

Ci sono due importanti limitazioni.

1. Molte regioni hanno estese coperture nuvolose, ed il mare non é visibile.
2. Il flusso é principalmente parallelo ai fronti di temperatura, e le correnti forti possono esistere lungo i fronti anche se i fronti non si muovono;é quindi essenziale tracciare il moto di piccoli vortici intrappolati nel flusso vicino al fronte e non la posizione del fronte.

Lo Spargimento delle Anatre di Plastica
Il 10 gennaio 1992 un container (ISO30 di 12.2m) contenente 29,000 giocattoli da bagno (incluse le anatre di plastica) cadde fuoribordo da una nave portacontainer a circa 44.7°N, 178.1°E. Dieci mesi più tardi i giocattoli cominciarono a spiaggiare vicino Sitka, Alaska. Un incidente simile il 27 maggio 1990 rilascio 80,000 scarpe della Nike a 48°N, 161°W quando le onde sciacquarono i container della Hansa Carrier (Figure 10.17). Lo sversamento e l'eventuale recupero dei giocattoli fornirono un buon esame per il modello numerico sviluppato da Ebbesmeyer and Ingraham (1992, 1994) per calcolare le traiettorie di sversamenti di petrolio. Loro calcolarono le possibili traiettorie delle anatre di plastica perse usando il modello numerico Ocean Surface Current Simulations (OSCURS) forzato dai venti calcolati dai dati giornalieri di pressione al livello del mare forniti dal Fleet Numerical Oceanography Center. Le traiettorie calcolate coincidevano bene con i luoghi di ritrovamento sulla spiaggia. Usando un aumento dell'influenza del vento del 50% ed un decremento del 5% nella funzione dell'angolo di deflessione, i giocattoli arrivano vicini Sitka al tempo del primo ritrovamento: il 16 novembre 1992.

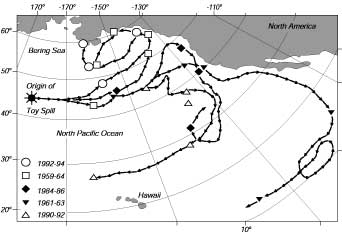
Figura 10.17 Traiettorie che le anatre di plastica perse dovrebbero aver seguito cadendo in acqua il 10 gennaio di anni differenti. Cinque traiettorie sono mostrate da un set di 48 simulazioni della perdita, ogni anno dal 1946 al 1993. Le traiettorie iniziano il 10 gennaio e finiscono due anni più tardi (simboli neri). I simboli grigi indicano le posizioni del 16 novembre dell'anno della perdita. Quindi i cerchi grigi indicano la posizione dove le anatre di plastica arrivarono alla spiaggia vicino Sitka. Il codice in basso a sinistra dà le date delle traiettorie. Da Ebbesmeyer and Ingraham (1994).

10.9 Misure di Correnti Euleriane

Le tecniche Euleriane hanno usato molti tipi differenti di correntometri attaccati a molti tipi di ormeggi o di navi.

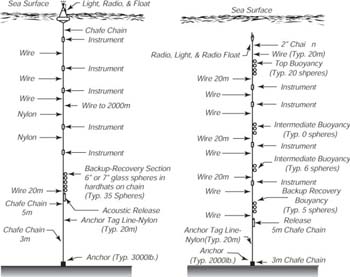
Gli ormeggi (Mooring) (Figura 10.18) sono posizionati sul fondo del mare o su navi. I mooring possono rimanere per mesi e più a lungo di un anno. Poiché i mooring devono essere posizionati e recuperati da navi da ricerca per mare profondo, la tecnica é costosa. L'ormeggio sommerso mostrato sulla destra della figura é preferito per molte ragioni: il galleggiante sommerso non é sottoposto alle forti correnti superficiali ad alta frequenza; l'ormeggio non é in vista e non attrae l'attenzione dei maleintenzionati; e poi il galleggiante é generalmente profondo abbastanza per evitare di essere preso dalle reti da pesca (non é così in Adriatico). Le misure fatte dai mooring hanno errori dovuti a:

1. Movimento del mooring. Gli ormeggi sommersi si muovono di meno. I mooring di superfice nelle correnti forti si muovono molto e sono usati raramente.
2. Campionamento inadeguato. Gli ormeggi tendono a non durare abbastanza per dare stime accurate della velocità media o della variabilità interannuale della velocità.
3. La crescita degli organismi marini (fouling) nei sensori, specialmente negli strumenti vicini alla superfice posizionati da qualche settimana.

Figura 10.18 Sinistra: Un esempio di ormeggio di superfice usato dal Gruppo Boe del Woods Hole Oceanographic Institution. Destra: Un esempio di ormeggio sommerso usato dallo stesso gruppo. Da Baker (1981).

Profilatori e Correntometri ad Effetto Doppler
Le più comuni misure Euleriane di corrente sono fatte usando il suono. Tipicamente, il correntometro profilatore trasmette il suono in tre o quattro raggi puntati in differenti direzioni. Il plankton e le piccole bolle riflettono il suono indietro allo strumento. Lo spostamento Doppler del suono riflesso é proporzionale alla componente radiale della velocità di ciò che riflette il suono. Dal combinare i dati di tre o quattro trasduttori, la velocità orizzontale della corrente é calcolata assumendo che il plankton e le bolle non si muovono molto relativamente all'acqua.

Due tipi di correntometri acustici sono per lo più usati. Lo Acoustic-Doppler Current Profiler, chiamato ADCP, misura lo spostamento Doppler del suono riflesso a varie distanze dallo strumento usando i raggi del suono proiettati nell'acqua proprio come un radar misura le distanze dal tempo impiegato per essere riflesso indietro. I dati dei raggi sono combinati per dare i profili della velocità di corrente in funzione della distanza dallo strumento. Sulle navi, i raggi sono puntati diagonalmente verso il basso a 3–4 angoli orizzontali relativamente alla prua della nave. Gli strumenti montati sul fondo usano raggi puntati diagonalmente verso l'alto.

Gli strumenti montati a bordo delle navi sono molto usati per profilare le correnti dei primi 200-300 m della superfice marina mentre la nave si muove tra le stazioni idrologiche. Poiché la nave si muove relativamente al fondo, la velocità e l'orientazione della nave deve essere accuratamente conosciuta. I dati GPS hanno fornito queste informazioni fin dall'inizio del 1990.

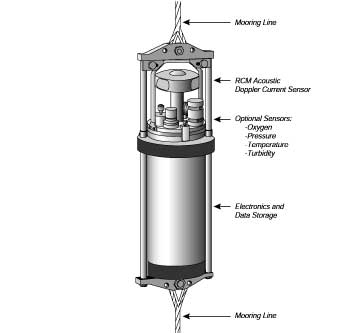
I correntometri acustici ad effetto Doppler sono molto più semplici degli ADCP. Trasmettono in continuo impulsi sonori per misurare la velocità della corrente ad una distanza di un metro. Sono posizionati su mooring, qualche volta sul CTD. Gli strumenti sugli ormeggi registrano la velocità in funzione del tempo per molti giorni o mesi. Il correntometro Aanderaa nella figura 10.19 é un esempio di questo tipo. Gli strumenti sui CTD profilano le correnti dalla superfice fino al fondo delle stazioni idrologiche.

Figura 10.19 Un esempio di correntometro ormeggiato, il modello RCM 9 prodotto dalla Aanderaa Instruments. Le due componenti della velocità orizzontale sono misurate da un correntometro acustico, le direzioni sono riferite al nord usando una bussola ad effetto Hall. L'elettronica, il registratore dei dati e la batteria sono allocate nell'ollogiamento resistente alla pressione. La accuratezza é di ± 0.15 cm/s e ±5° (Da Aanderaa Instruments).

Tomografia Acustica
Un'altra tecnica acustica usa segnali sonori trasmessi nel canale acustico verso e da ormeggi sparsi su regioni oceaniche. La tecnica é costosa perché richiede molti ormeggi profondi e sorgenti sonore potenti. Promette, comunque, di avere informazioni difficili con altri mezzi. Il numero di cammini acustici in una regione cresce con il quadrato del numero di mooring. E il segnale che si propaga lungo il canale sonoro ha molti modi, alcuni sono vicino all'asse del canale, altri si propagano vicini alla superfice ed al fondo del canale (vedi Figura 3.16). I vari modi danno la struttura verticale della temperatura nell'Oceano, ed i molti cammini nell'orizzontale danno la distribuzione spaziale della temperatura. Se un ormeggio ritrasmette il segnale che riceve da un altro ormeggio, il tempo per il segnale di propagarsi in una direzione meno il tempo per il segnale di propagarsi nella direzione opposta, il tempo di viaggio reciproco, é proporzionale alla componente della corrente parallela al cammino acustico.

10.10 Concetti importanti

1. La distribuzione della pressione é quasi precisamente la pressione idrostatica ottenuta assumendo l'Oceano fermo. La pressione é quindi calcolata molto precisamente dalle misure di temperatura e conducbilità in funzione della pressione usando l'equazione di stato dell'acqua marina. I dati idrologici danno il campo relativo della pressione interna dell'Oceano.
   
   
2. Il flusso nell'Oceano é quasi esattamente in bilancio geostrofico, eccetto per il flusso negli strati limite superiore ed inferiore. La forza di Coriolis bilancia quasi esattamente i gradienti di pressione orizzontali.
   
   
3. Le osservazioni dei satelliti altimetrici della topografia dell'Oceano danno la superfice geostrofica. I calcoli della topografia richiedono un geoide accurato, che é conosciuto con sufficiente precisione soltanto su distanze ?? exceeding a few thousand kilometers ??. Se il geoide non é conosciuto, gli altimetri possono misurare i cambiamenti della topografia come una funzione del tempo, che forniscono le variazioni delle correnti geostrofiche superficiali.
   
   
4. Il Topex/Poseidon é il sistema altimetrico più preciso, e può misurare la topografia oppure le variazioni della topografia con una accuratezza di ± 4.7cm.
   
   
5. I dati idrologici sono usati per calcolare le correnti geostrofiche interne all'Oceano, relative ad una corrente nota ad un certo livello. Il livello può può essere quello delle correnti superficiali misurate dall'altimetria oppure un livello assunto di velocità zero a profondità di 1-2km.
   
   
6. Il flusso oceanico che é independente dalla profondità é detto flusso barotropico, quello che dipende dalla profondità é detto baroclino. I dati idrologici forniscono soltanto il flusso baroclino.
   
   
7. Il flusso geostrofico non può cambiare nel tempo, così il flusso nell'Oceano non é esattamente geostrofico. Il metodo geostrofico non si applica ai flussi nella zona dell'equatore perché lì la forza di Coriolis svanisce.
   
   
8. Le pendenze delle superfici a densità o temperatura costante in una sezione dell'Oceano possono essere usate per stimare la velocità del flusso attraverso la sezione.
   
   
9. Le tecniche lagrangiane misurano la posizione di una porzione di acqua nell'Oceano. La posizione può essere determinata usando boe alla deriva superficiali e profonde. Un'altra tecnica usa traccianti chimici come il trizio.
   
   
10. Le tecniche Euleriane misurano la velocità del flusso passante in un punto dell'Oceano. La velocità del flusso può essere misurata usando correntometri ormeggiati oppure con profilatori acustici di velocità posti sulle navi, su CTD o su ormeggi.