Capitolo 12 - La Vorticità

Molti dei fluidi scorrono in maniera familiare, dalle vasche da bagno alle piscine di nuoto, non sono rotanti, o ruotano cosi' lentamente che la rotazione non e' importante eccetto forse allo svuotamento della vasca quando l'acqua e' lasciata andare via. Come risultato, non abbiamo una bouna comprensione intuitiva dei flussi rotanti. Nell'Oceano, la rotazione e la conservazione della vorticita' influiscono fortemente su distanze piu' grandi di poche decine di kilometri. La consequenza della rotazione porta ai risultati che abbiamo visto prima nella nostra vita di tutti i giorni con i fluidi. Per esempio, vi siete mai chiesti perche' il rotore dello sforzo del vento risulta in un trasporto di massa nella direzione nord-sud e non in quella est-ovest? Che cosa ha di speciale il movimento nord-sud? In questo capitolo, andremo ad esplorare alcune conseguenze della rotazione di un flusso nell'Oceano.

12.1 La Definizione della Vorticità

In parole semplici, la vorticita' e' la rotazione del fluido. La quantita' della rotazione puo' essere espressa in vari modi. Consideriamo un catino di acqua poggiato su un tavolo in un laboratorio. L'acqua puo' ruotare nel catino. Oltre alla rotazione dell'acqua nel catino, il catino ed anche il laboratorio stanno ruotando perche' sono sulla Terra che ruota intorno al suo asse. I due processi sono separati, e possiamo considerare due tipi di vorticita'.

La Vorticita' Planetaria
Tutte le cose sulla Terra, inclusi gli oceani, l'atmosfera, ed il catino d'acqua ruotano con la Terra. Questa rotazione impartita dalla Terra e' la vorticita' planetaria f. Essa e' due volte la velocita' di rotazione della Terra:

(12.1)

La vorticita' planetaria e' il parametro di Coriolis che abbiamo usato in precedenza nella discussione del flusso nell'Oceano. E' piu' grande ai poli dove e' il doppio della rotazione terrestre. Notare che la vorticita' scompare all'equatore e nell'emisfero sud assume valori negativi perche' φ e' negativo.

La Vorticita' Relativa
L'Oceano e l'atmosfera non ruotano esattamente alla stessa velocita' della Terra. Essi hanno un genere di rotazione relativo alla Terra dovuto alle correnti ed ai venti. La Vorticita' Relativa ζ e' la vorticita' dovuta alle correnti nell'Oceano. Matematicamente e':

(12.2)

dove V = (u,v) e' il vettore della velocita' orizzontale, e dove abbiamo assunto che il flusso e' bi-dimensionale. Questo e' vero se il flusso si estende su distanze piu' grandi di poche decine di kilometri. z is the vertical component of the three-dimensional vorticity vector ω, ed e' qualche volta scritta ω_z. ζ e' positiva per rotazione anti-orarie viste da sopra. Questo e' lo stesso senso della rotazione terrestre nell'emisfero settentrionale.

Note sui SimboliI symboli comunemente usati in una parte dell'oceanografia spesso hanno molti significati differenti in altre parti. Qui usiamo ζ per la vorticita', ma nel Capitolo 10, usiamo ζ per intendere l'altezza della superfice marina. Potremmo usare ω_z per la vorticita' relativa, ma ω e' anche comunemente usata per intendere la frequenza in radianti al secondos. Ho tentato di eliminare molti usi che confondono, ma il doppio uso di ζ e' uno con il quale dobbiamo convivere. Fortunatamente, non dovrebbe causare molta confusione.

Per un corpo rigido rotante con velocita' Ω, il rotore V = 2Ω. Naturalmente, il flusso non ha bisogno di ruotare come un corpo rigido per avere vorticita' relativa. La vorticita' puo' anche risultare dallo shear. Per esempio, al confine occidentale nord/sud di un oceano, u = 0, v = v (x) e ζ = ∂v(x)/∂x.

ζ e' generalmente molto piu' piccola di f, ed e' piu' grande al limite delle correnti veloci come la Gulf Stream. Per avere un'idea della misura di ζ, consideriamo il bordo della Gulf Stream a largo di Capo Hatteras dove la velocita' diminuisce da 1 m/s in 100 km al confine. Il rotore della corrente e' approssimativamente (1 m/s)/(100 km) = 0.14 giri/giorno = 1 giro/settimana. Quindi perfino questa grande vorticita relative e' ancora quasi sette volte piu' piccola di f. Altri valori tipici di vorticita' relative, come la vorticita' degli "eddy", e' un giro al mese.

La Vorticita' Assoluta
La somma della vorticita' planetaria e di quella relativa e' chiamata vorticita' assoluta:

(12.3)

Possiamo ottenere un'equazione per la vorticita' assoluta manipolando semplicemente le equazioni del moto senza attrito. Cominciamo da:

	(12.4a)
	(12.4b)

Se espandiamo la derivata totale, e se sottraiamo ∂ /∂y della (12.4a) da ∂ /∂x della (12.4b) per eliminare i termini della pressione, otteniamo dopo alcuni passaggi algebrici:

(12.5)

Nel derivare la (12.15) usiamo:

ricordando che f e' independente dal tempo t e che la distanza verso est e' x.

Vorticita' Potentiale
La velocita' di rotazione di un cilidro di fluido cambia se il cilindro e' spanso o contratto. Questo cambia la vorticita' attraverso i cambi nella ζ. Per vedere come accade cio', consideriamo il flusso barotropic e geostrofico in un oceano con profondita' H(x, y, t), dove H e' la distanza dalla superfice marina al fondo. Quindi, permettiamo alla superfice di avere una topografia (Figura12.1).

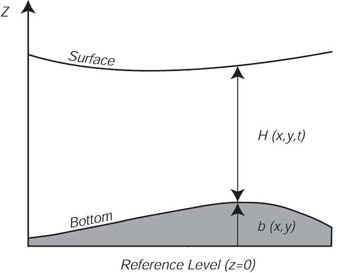Figura 12.1 Shema del flusso di un fluidousato per derivare la conservazione della vorticita' potentiale. Da Cushman-Roisin (1994).

Integrando l'equazione di continuita' (7.19) dal fondo alla superfice dell'oceano otteniamo (Cushman-Roisin, 1994):

(12.6)

dove b e' la topografia del fondo, e H e' la profondita' dell'acqua. Le condizioni al contorno richiedono che il flusso alla superfice ed al fondo siano lungo la superfice e lungo il fondo. Cosi' le velocita' verticali in alto e in basso sono:

	(12.7)
	(12.8)

Sostituendo la (12.7) e la (12.8) dentro la (12.6) otteniamo

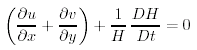Sostituendo questa dentro la (12.5) abbiamo:

che puo' essere scritta:

Le quantita' tra parentesi devono essere costanti. Questa e' chiamata vorticita' potentiale Π. La vorticita' potenziale e' conservata lungo una traiettoria del fluido:

(12.9)

Per un flusso baroclino in un fluido continuamente stratificato, la vorticita' potenziale puo' essere scritta (Pedlosky, 1987: § 2.5):

(12.10)

dove λ e' ogni conservata quantita' per ogni elemento del fluido. In, particolare, se λ = ρ allora:

(12.11)

assumendo che i gradiendi orizzontali della densita' sono piccoli comparati ai gradienti verticali, una buona assunzione nel termoclino. All'interno degli oceani, f >> ζ e la (12.11) e' scritta (Pedlosky, 1996, eq 3.11.2):

(12.12)

Questo permette alla vorticita' potenziale dei vari strati dell'oceano di essere determinata direttamente dai dati idrologici senza conoscere il campo delle velocita'.

12.2 La Conservazione della Vorticità

Il momento angolare di ogni corpo isolato che ruota e' conservato. Il corpo che ruota puo' essere un vortice dell'Oceano di una Terra nello spazio. Se il corpo ruotante non e' isolato, cioe', se e' legato ad un altro corpo, allora il momento angolare puo' essere trasferito tra i corpi. I due corpi non hanno bisogno di essere in contatto fisico. Le forze gravitazionali possono trasferire il momento tra i corpi nello spazio. Torneremo su questo argomento nel Capitolo 17 quando discuteremo delle maree dell'Oceano. Qui, guardiamo alla conservazione della vorticita' in un oceano ruotante.

L'attrito e' fondamentale per il trasferimento del momento in un fluido. L'attrito trasferisce momento dall'atmosfera all'Oceano attraverso il sottile, attritoso strato di Ekman layer alla superfice del mare. L'attrito trasferisce momento dall'Oceano alla Terraferma attraverso lo strato di Ekman al fondo del mare. L'attrito lungo i fianchi delle montagne sommerse portano a differenze di pressione nei lati delle montagne che causano un'altra forma di resistenza chiamata attrito di forma (form drag). Questo e' lo stesso attrito che causa la forza del vento su una automobile che viaggia a grande velocita'. Nel vasto interno dell'Oceano il flusso e', comunque, senza attrito, e la vorticita' e' conservata. Cosi' un flusso e' detto essere conservativo.

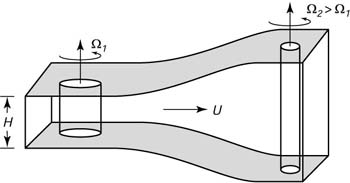Figura 12.2 Shema della produzione di vorticita' relativa dei cambiamenti di altezza di una colonna di fluido. Quando una colonna di fluido verticale si muove da sinistra verso destra, l'allungamento verticale riduce il momento di inerzia della colonna, facendola ruotare piu' velocemente.

Conservazione della Vorticita' Potenziale La conservazione della vorticita' potentiale unisce insieme i cambiamenti nella profondita', la vorticita' relativa, ed i cambiamenti nella latitudine. Tutti e tre interagiscono.

1. I cambiamenti nella profondita'H del flusso provocano variazioni nella vorticita' relativa. Il concetto e' analogo con il modo dei ballerini sul ghiaccio, che diminuiscono la loro velocita' di rotazione estendendo le loro braccia e gambe. Questa azione aumenta il loro momento di inerzio e fa' diminuire la velocita' di rotazione. (Figura 12.2).
2. I cambiamenti in latitudine richiedono un corrispondente cambiamento in ζ. Come una colonna di acqua si muove verso l'equatore, f diminuisce, e ζ deve deve diminuire (Figura 12.3). Se questo puo' sembrare talvolta misterioso, Von Arx (1962) suggerisce di considerare un barile di acqua a riposo al polo nord. Se il barile e' mosso verso sud, l'acqua che e' dentro mantiene la rotazione che aveva al polo e quindi dovrebbe ruotare in verso anti-orario nella nuova latitudine dove f e' piu' piccolo.

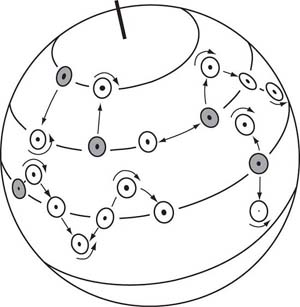Figura 12.3 Il momento angolare tende ad essere conservato quando la colonna d'acqua cambia latitudine. Questo provoca una variazione nella vorticita' relativa della colonna. Da Von Arx (1962).

Conseguenze della Conservazione della Vorticita' Potentiale
Il concetto di conservazione della vorticita' potentiale ha conseguenze che vanno lontano, e la sua applicazione porta ad una comprensione piu' profonda delle correnti oceaniche.

1. Nell'Oceano f tende ad essere molto piu' grande di ζ e cosi' f/H = constante. Questo richiede che il flusso in un oceano a profondita' costante sia zonale (lungo est-ovest). Naturalmente, la profondita' non e' costante, ma in generale, le correnti tendono ad essere est-ovest piuttosto che nord-sud. I venti producono solo delle piccole variazioni a ζ, portando ad una piccola componente meridionale nel flusso (vedi Figura 11.3).

2. I flussi barotropici sono deviati dalle caratteristiche del fondo marino. Consideriamo cosa accade al flusso che, dalla superfice al fondo, incontra una dorsale sottomarina (Figura 12.4). Come la profondita' diminuisce, anche la ζ + f deve diminuire ed il flusso e' deviato verso l'equatore. Questo e' detto Guida Topografica (topographic steering). Se la variazione in profondita' e' sufficientemente grande, nessun cambiamento in latitude sara' sufficiente a conservare la vorticita' potentiale, ed il flusso non potra' superare la dorsale. Questo e' detto blocco topografico (topographic blocking).

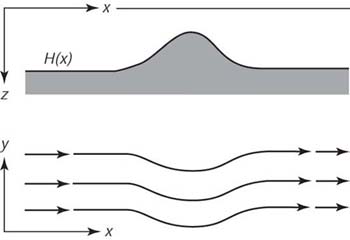Figure 12.4 Il flusso barotropic sopra una dorsale sottomarina e' deviato verso l'equatore per conservare la vorticita' potenziale. Da Dietrich, et al. (1980).

3. Il bilancio della vorticita' fornisce una spiegazione alternativa all'esistenza delle correnti occidentali di bordo a scala di gyre (Figura 12.5). Consideriamo il flusso a scala di gyre in un bacino oceanico, diciamo l'Atlantico settentrionale da 10°N a 50°N. Il vento che soffia sopra l'Atlantico aggiunge vorticita' negativa. Come l'acqua fluisce intorno al gyre, la vorticita' del gyre deve rimanere quasi costante, altrimenti il flusso dovrebbe aumentare o diminuire. L'input di vorticita' negativa deve essere bilanciato da una sorgente di vorticita' positiva.

La sorgente di vorticita' positiva deve essere la corrente di bordo: il flusso forzato dal vento e' baroclino, che e' debole vicino al fondo, cosi' l'attrito del fondo non puo' trasferire fuori dall'oceano la vorticita'. Quindi, dobbiamo decidere quale confine contribuisce. I flussi tendono ad essere zonali(lungo est-ovest), ed i confini est-ovest non possono risolvere il problema. Ad oriente, la vorticita' potentiale e' conservata: l'input di vorticita' relativa negativa e' bilanciato da una diminuizione nella vorticita' petenziale quando il flusso gira verso sud. Soltanto ad ovest la vorticita' non e' bilanciata, ed una forte sorgente di vorticita' positiva e' richiesta. La vorticita' e' fornita dallo 'current shear' nel confine occidentale quando la corrente sfrega sulla costa producendo una velocita' verso nord che e' zero sulla costa (Figura 12.5, destra).

In questo esempio, l'attrito trasferisce momento angolare dal vento all'oceano e la viscosita' vorticosa -attrito- trasferisce momento angolare dall'oceano alla Terraferma.

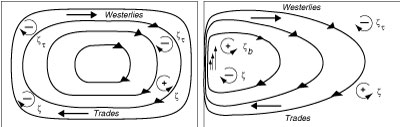Figura 12.5 Il bilancio della vorticita' potentiale puo' chiarire perche' le correnti occidentali di bordo sono necessarie. Sinistra: L'input di vorticita' del vento ζt bilancia la variazione di vorticita' relativa ζ ad est quando il flusso si muove verso sud e f diminuisce; ma i due non si bilanciano ad ovest dove ζ deve diminuire quando il flusso si muove verso nord e f aumenta. Destra: La vorticita' ad ovest e' bialanciata dalla vorticita' relativa ζb generata dallo shear nella corrente occidentale.

12.3 La Vorticità e la Pompa di Eckman

La rotazione piazza un'altro vincolo molto interessante al campo di flusso geostrofico. Per aiutarvi a capire i vincoli, consideriamo prima un flusso in un fluido con rotazione costante. Poi guarderemo come la vorticita' vincola un flusso di un fluido ruotante, che varia con la latitudine. Una comprensione dei vincoli porta ad una conoscenza piu' profonda dei risultati di Sverdrup e di Stommel discussi nel precedente capitolo.

La dinamica del fluido sul f plane: Il Teorema di Taylor-Proudman
L'influenza della vorticita' dovuta alla rotazione terrestre e' molto stringente per un flusso di un fluido a densita' costante ρ₀ su un piano a rotazione costante f = f₀. Dal Capitolo 10, le tre compnenti delle equazioni geostrofiche (10.4) sono:

	(12.13a)
	(12.13b)
	(12.13c)

e l'equazione di continuita' (7.19) e':

(12.13d)

Facendo la derivata in z della (12.13a) ed usando (12.13c) abbiamo:

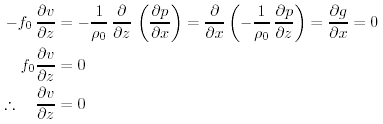In maniera simile, per la componente u della velocita' (12.13b). Cosi', la derivata verticale del campo di velocita' orizzontale deve essere zero.

(12.14)

Questo e' il Teorema di Taylor-Proudman, che si applica a flussi che variano lentamente in fluidi omogenei, senza attrito e ruotanti. Il teorema pone forti vincoli al flusso:

Se therefore any small motion be communicated to a rotating fluid the resulting motion of the fluid must be one in which any two particles originally in a line parallel to the axis of rotation must remain so, except for possible small oscillations about that position - Taylor (1921).

Quindi, la rotazione rende molto piu' difficile il flusso! Il flusso geostrofico non puo' passare sopra un mote sottomarino, deve girarci intorno. Taylor (1921) derivo' la (12.14) direttamente e dopo la (12.16) below. Proudman (1916) derivo' independentemente lo stesso teorema ma non cosi' esplicitamente.

Altre conseguenze del teorema possono essere ottenute eliminando i termini della pressione dalla (12.13a & 12.13b) per ottenere:

	(12.15a)
	(12.15b)
	(12.15c)

Poiche' il fluido e' incompressibile, l'equatione di continuita' (12.13d) richiede

(12.16)

Inoltre, poiche' w = 0 alla superfice ed al fondo, se il fondo e' piatto, la' non ci puo' essere velocita' verticale sul f-plane. Notare che la derivazione della (12.16) non richiede che la densita' sia constante. Richiede soltanto un moto lento in un fluido ruotante e senza attrito.

Dinamica dei Fluidi su un Piano Beta: La Pompa di Ekman
Se la (12.16) e' vera, il flusso non puo' espandersi o contrarre nella direzione verticale, ed ' quindi rigido come una barra di ferro. Non ci puo' essere nessun gradiente di velocita' verticale in un oceano con vorticita' planetaria costante. Allora come puo' la divergenza del trasporto di Ekman al livello del mare portare a velocita' verticali alla superfice o alla base dello strato di Ekman? La risposta puo' soltanto essere che uno dei vincoli usati nella derivazione della (12.16) deve essere violata. Un vincolo che puo' essere sciolto e' la richiesta che f = f₀.

Consideriamo allora il flusso su un piano beta. Se f = f₀ + β y, allora (12.15a) becomes:

	(12.17)
	(12.18)

dove abbiamo usato la (12.13a) per ottenere v nel lato destro della (12.18).

Usando l'equazione di continuita', e ricordando che β y << f₀

(12.19)

dove abbiamo usato il sub-scritto G per enfatizzare che la (12.19) si applica all'interno del flusso geostrofico oceanico. Cosi' la variazione della forza di Coriolis con la latitudine permette i gradienti verticali di velocita' all'interno geostrofico dell'Oceano, e la velocita' verticale porta alle correnti nord-sud. Questo spiega perche' Sverdrup e Stommel hanno avuto bisogno di un β-plane per i loro calcoli.

La Pompa di Eckman nell'Oceano
Nel Capitolo 9, abbiamo visto che il rotore dello sforzo del vento T produce una divergenza del trasporto di Ekman che porta ad una velocita' verticale w_E(0) alla sommita' dello strato di Eckman. Nel Capitolo 9 abbiamo derivato

(12.20)

che e' (9.30b) dove ρ e' la densita' e f e' il parametro di Coriolis. Poiche' la velocita' verticale alla superfice del mare deve essere zero, la velocita' verticale di Ekman deve essere bilanciata dalla velocita' geostrophic verticale w_G(0).

(12.21)

La Pompa di Ekman ( w_E(0) ) guida la corrente geostrofica verticale (-w_G (0) ) all'interno dell'Oceano. Ma perche' questo produce la corrente verso nord calcolata da Sverdrup (11.6)? Peter Niiler (1987: 16) fornisce questa semplice spiegazione.

Postuliamo che esiste un livello profondo dove il moto orizzontale e verticale dell'acqua e' molto ridotto da quello che c'e' subito sotto lo strato rimescolato (Figure 12.6)... Assumiamo inoltre, che li', la vorticita' sia conservata (oppure che il mescolamento sia piccolo) e che il flusso sia cosi' lento che le accelerazioni sulla superfice terrestre siano molto piu' piccole di quelle di Coriolis. In una tale situazione una colonna d'acqua di altezza H conservera' la sua rotazione per unita' di volume, f /H (relativa al Sole, parallela all'asse di rotazione terrestre). La colonna vorticosa che e' compressa alla sommita' dal vento forzante, sprofonda (H diminuisce) e l'acqua al fondo e' in una relativa calma dovrebbe tendere ad abbassarsi ed a diminuire la sua rotazione. Ma a causa della superfice curva dell'oceano, si dovrebbe muovere verso sud (oppure estendere la sua colonna) per riguadagnare rotazione. Quindici dovrebbe essere un grande flusso di acqua ad una certa profondita' sotto la superfice al sud dove in aree dove gli strati supeficiali producono un moto di sprofondamento ed al nord dove il moto di risalita e' prodotto. Questo fenomeno fu modellato correttamente per la prima volta da Sverdrup (1947) (dopo la scrittura di "Oceans") e fornisce una spiegazione dinamicamente plausibile di come il vento produce la circolazione profonda nell'Oceano.

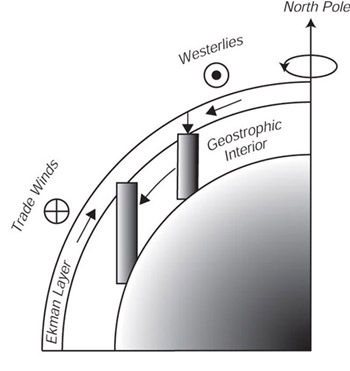Figura 12.6 La pompa di Ekman che produce una velocita' alla base dello strato di Ekman forza il fluido all'interno dell'Oceano a muoversi verso sud. Da Niiler (1987).

Peter Rhines (1982) sottolinea che the la rigida colonna di acqua cerca di uscire dalla compressione imposta dall'atmosfera muovendosi verso sud. La velocita' meridionale e' circa 5,000 volte piu' grande della velocita' verticale di Ekman.

La Pompa di Ekman: Un Esempio
Ora vediamo come la pompa di Ekman indirizza in flusso geostrofico nel Pacifico centrale del nord (Figura 12.7) dove il rotore dello sforzo del vento e' negativo. I venti occidentali (Westerlies) dell'emisfero nord forzano un trasporto verso sud, gli alisei del sud forzano un trasporto verso nord. I trasporti convergenti di Ekman devono essere bilanciati dalla velocita' geostrofica verso il basso (12.21).

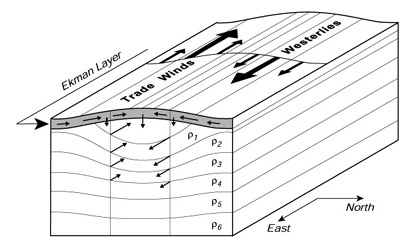Figura 12.7 I venti alla superfice del mare forzano i trasporti di Ekman a destra del vento nell'emisfero nord dell'esempio (le frecce piene nello strato di Ekman ombreggiato). I trasporti convergenti di Ekman forzati dagli alisei e dai venti occidentali guidano un flusso geostrofico verso il basso propio sotto lo strato di Ekman (frecce verticali piene), portando ad curvamento verso il basso delle isolinee della densita' ri. Le correnti geostrofiche associate all'acqua calda sono contrassegnate dalle frecce piene. Da Tolmazin (1985).

Poiche' l'acqua vicino la superfice e' piu' calda di quella profonad, la velocita' verticale produce un corpo di acqua calda. Piu' in profondita' nell'Oceano, la corrente geostrofica guidata dal vento va a zero (ipotesi di Sverdrup) e i gradienti profondi di pressione devono andare essere zero. Risulta che, la superfice dovrebbe sollevarsi verso l'alto perche' una colonna di acqua calda e' piu' alta di una fredda che ha lo stesso peso (devono avere lo stesso peso, altrimenti, la pressione profonda non sarebbe costante, e ci sarebbe un gradiente profondo orizzontale). Una tale distribuzione di densita' produce gradienti di pressione nord-sud alle medie profondita' che deve essere bilanciato dalle correnti geostrofiche nord-sud. In parole povere, la divergenza dei trasporti di Ekman ridistribuisce la massa alll'interno senza attrito dell'Oceano generando le correnti geostrofiche forzate dal vento.

Ora continuiamo con l'idea di includere l'intero Pacifico settentrionale per vedere come i venti producono correnti che fluiscono contro-vento. L'esempio fornira' una comprensione piu' profonda dei risultati di Sverdrup discussi nel §11.1.

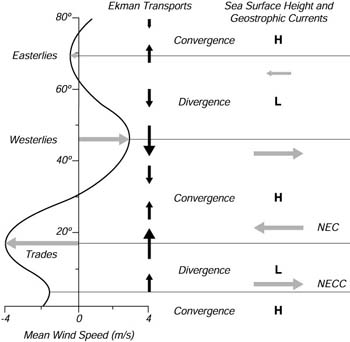
La figura 12.8 mostra i venti medi nord-sud nel Pacifico, insieme con i trasporti nord-sud di Ekman forzati dai venti. Da Notare che la convergenza dei trasporti porta a down-welling, che produce uno strato spesso di acqua calda nel primo kilometro della colonna d'acqua, ed un alto livello del mare. Figura 12.6 e' uno schema della sezione trasversale della regione tra 10°N e 60°N, e mostra il corpo di acqua calda nel primo kilometro centrato su 30°N. Al contrario, trasporti divergenti producono bassi livelli del mare. I gradienti di pressione medi nord-sud associati con le alte e basse sono bilanciati dalla forza di Coriolis delle correnti geostrofiche est-oest alla superfice dell'Oceano (mostrato alla destra nella figura).

Figura 12.8 Un esempio di come i venti producono le correnti geostrofiche che viaggiano contro-vento. I trasporti di Ekman dovuti ai venti nel Pacifico settentrionale (Sinistra) portano alla pompa di Ekman (Centro), che creano i gradienti di pressione nord-sud nello strato superficiale dell'Oceano. I gradienti di pressione sono bilanciati dalla forza di Coriolis dovuta alle correnti geostrofiche est-ovest (Destra). le linee orizzontali indicano regioni dove il rotore dello sforzo del vento est-ovest cambia segno. AK: Alaskan Current, NEC: North Equatorial Current, NECC: North Equatorial Counter Current.

12.4 Concetti Importanti

1. La vorticita' confina fortemente la dinamica dell'Oceano.
   
   
2. La vorticita' dovuta alla rotazione terrestre e' molto piu' grande delle altre sorgenti di vorticita'.
   
   
3. Taylor e Proudman mostrarono che la velocita' verticale e' impossibile in un flusso con rotazione costante. L'Oceano e' rigido nella direzione parallela all'asse di rotazione. Percio' la pompa di Ekman richiede che la vorticita' planetaria varia con la latitudine. Questo spiega perche' Sverdrup e Stommel trovarono che la realistica circolazione oceanica, che e' guidata dalla pompa di Ekman, richiede che f varii con la latitudine.
   
   
4. Il rotore dello sforzo del vento aggiunge vorticita' relativa ai gyre centrali di ogni bacino oceanico. Per circolazioni a stato stazionario nel gyre, l'oceano deve perdere vorticita' nelle correnti occidentali di bordo (western boundary currents).
   
   
5. Il rotore positivo dello sforzo del vento porta ad un flusso divergente nello strato di Ekman. La circolazione geostrofica all'interno degli oceani si aggiusta attraverso un trasporto di massa verso Nord.
   
   
6. La conservazione assoluta della vorticita' in un oceano con densita' constante porta alla conservazione della vorticita' potenziale. Cosi' i cambiamenti nella profondita' in un oceano con densita' costante richiedono cambiamenti di latitudine della corrente.