Capitolo 15 - Modelli Numerici

Abbiamo visto molto presto che le soluzioni analitiche delle equazioni del moto sono difficile o impossibili da risolvere per dei flussi tipici dell'Oceano. Il problema e' dovuto ai termini non-lineari, all'attrito ed alla necessita' di una forma reale del fondo marino e della linea di costa. Abbiamo anche visto come sia difficile descrivere l'Oceano dalle misure. I satelliti possono osservare alcuni processi quasi dovunque ad intervallo di pochi giorni. Ma osservano solo alcuni processi, e soltanto vicino la superfice. Le navi possono misurare molti piu' parametri, ed in profondita', ma le misure sono disperse. Quindi, i modelli numerici forniscono la sola utile visione globale delle correnti oceaniche. Discutiamo ora sull'accuratezza e la validita' dei modelli, tenendo in mente che sebbene sono solo modelli, essi forniscono una visione dell'Oceano realistica e notevolmente dettagliata.

15.1 Introduzione–Alcune Parole di Cautela

I modelli numerici delle correnti oceaniche hanno molti vantaggi. Simulano i flussi dei realistici bacini oceanici con dei realistici fondi marini. Includono l'influenza della viscosita' e delle dinamiche non-lineari. Possono anche calcolare i possibili flussi futuri dell'Oceano. Ma la cosa piu' importante, interpolano tra le sparse osservazioni dell'Oceano fornite dalle navi, dai drifter e dai satelliti.

I modelli numerici non sono senza problemi.

C'e' un bel po' di differenza tra il carattere di leggi fondamentali, da un lato, e la natura dei calcoli richiesti per dagli vita, dall'altro.
Berlinski (1996).

I modelli non possono dare descrizioni complete dei flussi oceanici anche se le equazioni sono accuratamente integrate. I problemi vengono da varie sorgenti.

Le equazioni discrete non sono la stessa cosa di quelle continue
Nel Capitolo 7 abbiamo scritto le equazioni differenziali che descrivono il moto di un flusso continuo. I modelli usano approssimazioni algebriche delle equazioni differentiali. Assumiamo che i bacini oceanici siano riempiti con una griglia di punti, e che il tempo si muove in avanti a piccoli passi. I valori della corrente, della pressure, della temperature, e della salinita' sono calcolati dai valori dei punti vicini ed al tempo del passo precedente. Ian Stewart (1992), un noto matematico, sottolinea che:

La discretizzazione e' essenziale per l'implementazione dei modelli ai computer e non possiamo fare a meno di cio'. L'essenza della difficolta' e' che la dinamica dei sistemi discreti e' relazionata soltanto vagamente a quella dei sistemi continui- quindi la dinamica dei sistemi discreti e' lontana dall'essere piu' dettagliata di quella delle controparte continua - e le approssimazioni usate possono creare soluzioni spurie.

I calcoli della turbolenza sono difficili
I modelli numerici forniscono informazione soltanto ai punti della griglia del modello. Essi non forniscono informazione sul flusso tra i punti. Inoltre, l'Oceano e' turbolento, e ogni modello oceanico capace di risolvere la turbolenza ha bisogno che i punti della griglia siano distanti alcuni millimetri, con il passo temporale di pochi millisecondi.

I modelli oceanici utilizzati hanno i punti della griglia spaziati da decine a centinaia di kilometri in orizzontale, e da decine a centinaia di metri in verticale. Questo comporta che la turbolenza non puo' essere calcolata direttamente, e che l'influenza della turbolenza deve essere parametrizzata. Holloway (1994) afferma coincisivamente il problema:

I modelli oceanici fissano molti gradi di liberta' in meno dell'Oceano reale (intorno ai 20 ordini di grandezza). We compensate by applying ' eddy-viscous goo' to squash motion at all but the smallest retained scales. (Usiamo anche approssimazioni numeriche non conservative.) Questo e' analogo a mettere una parete in una scatola per impedire alle molecole del gas di invadere l'altro spazio della scatola. I nostri modelli oceanici non possono invadere molti dei gradi di liberta' dell'Oceano reale semplicemente perche' i modelli non li includono.

Dando per scontato che non possiamo fare le cose "giuste", cio' e' meglio che che non fare nulla? That is not an option. "niente" significa means applying viscous goo and wishing for the ever bigger computer. Possiamo fare qualcosa di meglio? Per esempio, possiamo can we guess a higher entropy configuration attraverso cui i vortici (eddies) tendono a guidare l'Oceano (that tendency to compete with the imposed forcing and dissipation)?

Per "gradi di liberta'" Holloway vuole dire tutti i possibili moti: dalle onde piu' piccole e dalla turbolenza alle correnti piu' grandi. Fatemi fare un semplice conto. Sappiamo che l'Oceano e' turbolento con vortici anche di pochi millimetri. Per descrivere completamente l'Oceano abbiamo bisogno di un modello con i punti della griglia spaziati di 1mm apart e passi temporali di circa 1 ms. Il modello poi, deve avere 360° × 180° × (111 km/degree)² × 10¹² (mm/km)² × 3 km × 10⁶ (mm/km) = 2.4 × 10²⁷ punti di dati per almeno 3km di oceano profondo che copre tutto il globo. Il "global Parallel Ocean Program Model" descritto nella prossima sezione ha 2.2 × 10⁷ punti. Cosi' abbiamo bisogno di 10²⁰ volte piu' punti per descrivere l'Oceano reale. Qusti sono i 10²⁰ gradi di liberta' mancanti.

I modelli pratici devono essere piu' semplici dell'Oceano reale.
I modelli dell'Oceano devono girare sui computer odierni. Questo comporta che gli oceanografi semplifica ulteriormente i loro modelli. Usiamo le approssimazioni idrostatiche e di Boussinesq, e spesso usiamo le equazioni integrate in verticale, le equazioni di acqua poco profonda (Haidvogel e Beckmann, 1999: 37).Facciamo cio' perche' non possiamo ancora far girare i modelli piu' dettagliati della circolazione oceanica per migliaia di anni allo scopo di studiare il ruolo dell'Oceano nel clima globale.

I programmi numerici hanno errori
Conoscete qualche programma immune da bachi? I modelli numerici usano molte subroutine ognuna con molte linee di codice che sono convertite in istruzioni comprensibili ai processori, i programmi di conversione sono chiamati compilatori. Eliminare tutti gli errori del software e' impossibile. Con prove accurate, gli output possono essere corretti, ma l'accuratezza non puo' essere garantita. Inoltre, i calcoli numerici non possono essere piu' precisi dell'accuratezza dei numeri a virgola mobile e degli interi usati dai computer. Gli errori di arrotondamento non possono essere ignorati. Lawrence et al. (1999), esaminando gli output di un modello numerico dell'atmosphera trovo' un errore nel codice prodotto da un compilatore di FORTRAN-90 usato nei CRAY Research supercomputer usati per girare il codice. Trovarono anche errori di arrotondamento nella concentrazione dei traccianti calcolati dal modello. Entrambi gli errori produceva errori importanti nelle output del modello.

Molti modelli sono stati verificati e/o validati (Post and Votta, 2005). Quindi, senza adeguate verifiche e validazioni, gli output da modelli numerici non sono credibili.

Summario
Nonostante tutte queste sorgenti di errore, molte delle quali piccole nella pratica, i modelli numerici dell'Oceano stanno dando le visioni disponibili agli oceanografi, piu' dettagliate e complete della circolazione. Alcune delle simulazioni contengono dettagli del flusso mai visti. Langer (1999), parlando dell'uso dei computer in fisica, scrive:

Tutti coloro che sono implicati nelle scienze, sanno che il calcolatore e' diventato un mezzo fondamentale per la ricerca... I calcoli scientifici hanno raggiunto il punto in qui sonno alla pari con gli esperimenti di laboratorio e la teoria matematica come mezzo di ricerca nelle scienze e nell'ingiegneria,
Da Langer (1990).

Ho incluso le parole di avvertimento non per portare il lettore a credere che i modelli sono inutili, ma per accettare gli output "cum grano salis".

15.2 I Modelli Numerici in Oceanografia

I modelli numerici sono usati per molti scopi in oceanografia. Per la nostra discussione possiamo divide i modelli in due classi:

Modelli meccanicistici sono modelli semplificati usati per lo studio di processi. Poiche' i modelli sono semplificati, l'output e' piu' facile da interpretare di quello dei modelli complessi. Sono stati sviluppati molti tipi differenti di modelli semplificati, che includono i modelli per descrivere le onde planetarie, l'interazione del flusso con le caratteristiche del fondo marino, oppure la risposta dell'Oceano superficiale al vento. Questa e' forse la cosa piu' utile dei modelli, perche' fornisce una visione dei meccanismi fisici che influenzano l'Oceano. Lo sviluppo e l'uso di modelli meccanicistici , e' comunque oltre lo scopo di questo libro.

Modelli di Simulazione sono usati per calcolare una realistica circolazione delle regioni oceaniche. I modelli sono spesso molto complessi perche' includono tutti i processi importanti, e l'output e' difficile da interpretare.

Il primo modella di simulazione fu sviluppato da Kirk Bryan e Michael Cox al laboratorio di Geophysical Fluid Dynamics a Princeton. Il loro modello (Bryan, 1969) calcolava il flusso in tre dimensioni nell'Ocean usando l'equazione di continuita' e del momento con l'approssimazione idrostatica e di Boussinesq, e una equazione di stato semplificata. Tali modelli sono detti alle equazioni primitive (primitive equation) perche' usano le equazioni del moto molto basilari, o nella forma primitiva. L'equazione di stato permette al modello di calcolare i cambiamenti in densita' dovuti ai flussi di calore e di acqua attraverso la superfice del mare, in tal modo il modello include i processi termodinamici.

Il modello di Bryan-Cox usava una forte viscosita' e diffusione orizzontale e verticale per eliminare i vortici turbulenti con un diametro piu' piccolo di circa 500 km, che e' poco piu' di pochi punti della griglia del modello. Aveva una linea di costa complessa, caratteristiche smussate del fondale marino, ed una rigida condizione alla superfice. La rigida superfice era necessaria per eliminare le onde di superfice, come maree e tsunami, che si muovono troppo velocemente per il passo temporale grossolano usato in tutte le simulazioni del processo. La superfice rigida ha, comunque, degli svantaggi. Le isole rallentavano fortemente i calcoli, e le caratteristiche del fondo furono smussate per eliminare i gradienti troppo pronunciati.

La prima simulazione del modelo era regionale. Fu subito seguita da un modello globale (Cox, 1975) con una risoluzione orizzontale di 2° e con 12 livelli sulla verticale. Il modello girava ancora troppo lentamente anche sul piu' veloce computer di oggi, ma getto' le basi per i piu' recenti modelli. La grossolana risoluzione spaziale richiedeva grandi valori per la viscosita', e perfino i modelli regionali erano troppo viscosi per avere correnti occidentali realistiche e vortici di mesoscala.

Fin da quei tempi, il traguardo e' stato di produrre modelli con risoluzione piu' alta, modellazione piu' realistica dei processi fisici, e schemi numerici migliori. La tecnologia informatica sta cambiando rapidamente, ed i modelli si stanno evolvendo altrettando rapidamente. Gli output dai modelli piu' recenti del Nord Atlantico, che hanno una risoluzione di 0.03°, sembrano molto simili all'Oceano reale. I modelli di altre regioni della Terra mostrano correnti precedentemente sconosciute vicino all'Australia e nell'Atlantico del sud.

Modelli di Oceano e Atmosfera usano una spaziatura dei punti di griglia molto differente. Come conseguenza, i modelli oceanici ritardano circa un decennio rispetto a quelli atmosferici ????. I vortici dominanti dell'Oceano sono 1/30 di quelli dell'atmosfera (le tempeste). Ma, le caratteristiche dell'Oceano si evolvono ad un tasso che e' circa 1/30 di quello dell'atmosfera. Cosi' i modelli oceanici che girano un anno, hanno 30 x piu' griglie di punti orizzontali dell'atmosfera, ma hanno 1/30 dei punti di passi temporali. Entrambi hanno lo stesso numero di livelli sulla verticale. Di conseguenza, i modelli oceanici girano 30 volte piu' lenti dei modelli atmosferici della stessa complessita'.

15.3 Modelli di Oceano Globale

Molti tipi di modelli globali sono largamenti usati in Oceanografia. Molti hanno i punti del grigliato spaziati di un decimo di grado, che e' sufficiente per risolvere i vortici di mesoscala, come quelli visti nelle Figure 11.10, 11.11, e 15.2, che hanno un diametro piu' grande di due o tre volte la distanza tra i punti della griglia. La risoluzione verticale e' tipicamente intorno ai 30 livelli. I modelli includono:

1. Coste realistiche e caratteristiche del fondo;
2. Flussi di calore ed acqua attraverso la superfice;
3. Dinamica dei vortici; e
4. La controcorrente atlantica lungo i meridiani.

Molti modelli assimilano i dati dei satelliti e delle boe usando le tecniche descritte nel §15.5. I modelli variano in complessita' da quelli che girano su computer da tavolo ai quelli che richiedono i piu' veloci computer del mondo.

Tutti i modelli devono girare per calcolare uno o due decadi di variabilita' prima di essere usati per simulare l'Oceano. Questa prova e' chiamata spin-up. Lo "spin-up" e' necessario perche' le condizioni per la densita', i flussi del momento e del calore attraverso la superfice marina, e le equazioni del moto non sono tutte consistenti. I modelli sono inizializzati a riposo con i valori di densita' degli atlanti di Levitus (1982) e integrati per una decade usando i valori medi annuali dello sforzo del vento, dei flussi di calore, e del flusso di acqua. Il modello puo' essere integrato per molti anni usando i valori mensili dello sforzo del vento, i flussi di calore, ed i flussi di acqua.

Il modello di Bryan-Cox porto' allo sviluppo di numerosi modelli che hanno fornito visioni impressionanti della circolazione globale dell'Oceano.

Modular Ocean Model ( MOM) dal Geophysical Fluid Dynamics Laboratory
E' il modello principalmente e largamente usato, originato dal codice di Bryan-Cox. Consiste di numerosi moduli che possono essere configurati per girare su computer molto differenti per modellare molti aspetti differenti della circolazione. Il codice sorgente e' gratis e libero, e' di dominio pubblico. Il modello e' largamente usato per studi climatici e per studiare la circolazione oceanica con ampio range di scale temporali e spaziali (Pacanowski e Griffies, 1999).

Poiche' MOM e' usato per indagare i processi che coprono un largo intervallo di scale temporali e spaziali, il codice ed il manuale sono molto grandi. Comunque, per un tipico modellista oceanico, non e' necessario imparare tutti i suoi aspetti. Anzi, MOM puo' essere visto come una citta' che cresce con quartieri molto differenti. Alcuni quartieri comunicano fra loro, alcuni sono mutualmente incompatibili, ed altri sono basicamente independenti. Questa diversita' e' gia' una sfida da coordinare e da mantenere. Infatti, durante gli anni, certi "quartieri'' sono stati abbandonati o fortemente rinnovati per varie ragioni.
Da Pacanowski e Griffies (1999).

Il modello usa le equazioni del momento, l'equazione di stato, e le approssimazioni idrostatica e di Boussinesq. I moti a scala di sotto-griglia sono ridotti dall'uso della viscosita' vorticosa La versione 4 del modello ha migliorato gli schemi numerici, una superfice libera, caratteristiche del fondo realistiche, e molti tipi di mescolamento che includono il mescolamento orizzontale lungo le superfici di densita' costante. Inoltre, puo' essere accoppiato a modelli atmosferici.

Parallel Ocean Program Model (POP)
Questo modello e' stato prodotto da Smith e colleghi al Los Alamos National Laboratory (Maltrud et al, 1998) e' un'altro modello largamente usato sviluppato dal codice originale di Bryan-Cox. Il modello include algoritmi numerici migliorati, coste realistiche, isole, e caratteristiche del fondo non smussate. Ha una griglia di 1280 × 896 punti equispaziati sulla proiezione di Mercator che si estende da 77°S a 77°N, con 20 livelli nella verticale. Cosi' ha 2.2 × 10⁷ punti con una risoluzione di 0.28° × 0.28° cos θ, che varia da 0.28° (31.25 km) all' equatore a 0.06° (6.5 km) alle latitudini piu' alte. La risoluzione media e' di circa 0.2°. Il modello e' forzato dallo sforzo del vento, dai flussi di calore e di acqua alla superfice del ECMWF (Barnier et al, 1995).

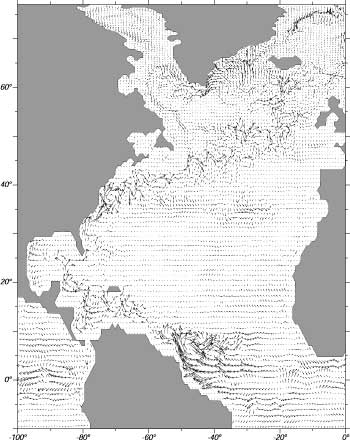Figura 15.1 Correnti geostrofiche, superficiali e sinottiche in Atlantico del 1 Ottobre, 1995 calcolate dal modello numerico Parallel Ocean Program sviluppato al Los Alamos National Laboratory. La lunghezza dei vettori e' proporzionale alla velocita' mediata nei primi 50m dell'Oceano. La direzione e' la direzione media della corrente. Da Richard Smith..

Hybrid Coordinate Ocean Model HYCOM
Tutti i modelli descritti finora usano le coordinate x, y, z. Tale sistema di coordinate ha vantaggi e santaggi. Puo' avere una alta risoluzione nello strato mescolato superficiale e nelle regioni poco profonde. Ma e' poco utile all'interno dell'Oceano. Sotto lo strato mescolato, il processo di mescolamento e' facile lungo le superfici a densita' costante e molto difficile attraverso tali superfici. Un sistema di coordinate piu' naturali all'interno dell'Oceano usa x, y, ρ, dove ρ e' la densita'. Tale modello e' detto un isopycnal model. Essenzialmente, ρ e' sostituita da z(ρ). Poiche' le superfici isopicne sono superfici a densita' costante, il mescolamento orizzontale e' sempre su superfici a densita' costante in questo modello.

Il modello HYCOM usa coordinate verticali diverse nelle differenti regioni dell'Oceano, combinando i migliori aspetti del modello a coordinata z ed a coordinata isopicna (Bleck, 2002). Il modello ibrido e' evoluto dal modello Miami Isopycnic-Coordinate Ocean (figura 15.2). E' un modello "primitive-equation" forzato dallo sforzo del vento e dai flussi di calore. Ha uno strato mescolato realistico e schemi di mescolamento orizzontale e vertuicale migliorato che include l'influenza delle onde interne, l'instabilita' dello shear, e la doppia diffusione (vedi §8.5). Il modello scaturisce dal lavoro di collaborazione tra ricercatori di molti laboratori oceanografici.

Figura 15.2 Output del modello Bleck’s Miami Isopycnal Coordinate Ocean Model MICOM. E' un modello ad alta risoluzione dell'Atlantic che mostra la Corrente del Golfo, la sua variabilita', e la circolazione del Nord Atlantico. Da Bleck.

Regional Oceanic Modelling System ROMS
Questo e' un modello regionale che puo' essere connesso in modelli di regioni piu' grandi. E' largamente usato per studiare i sistemi di correnti costiere strettamente legati al flusso di correnti piu' a largo, per esempio, la corrente della California. ROMS e' un modello idrostatico, ad equazioni primitive, che segue il fondo usando coordinate verticali allungate. Il modello e' forzato dai flussi di calore , di acqua e del momento orizzontali. Ha uno strato limite al fondo ed alla superfice migliorato (Shchepetkin e McWilliams, 2004).

Modelli Climatici
Sono usati per studi a grande scala di strutture idrografiche, dinamica del clima, e formazione di masse di acqua. Questi modelli sono gli stessi di quelli che permettono i vortici, a equazioni primitive che ho gia' descritto, eccetto che la risoluzione orizzontale e' molto piu' spaziata perche' devono simulare i processi oceanici per decenni e secoli. Quindi, devono avere una alta dissipazione per la stabilita' numerica, e non possono simulare i vortici di mesoscala. La risoluzione orizzontale tipica e' da 2° a 4°. I modelli tendono, comunque, ad avere una risoluzione verticale alta, necessaria per descrivere la circolazione profonda, molto importante per il clima.

15.4 Modelli Costieri

La forte importanza economica della zona costiera ha portato allo sviluppo di molti modelli numerici differenti per descrivere le correnti, le maree, e le 'acque alte' lungo la costa. I modelli vanno dalla spiaggia alla piattaforma continentale, e possono includere una superfice libera, coste e caratteristiche del fondo realistiche, apporti fluviali, e la forzante atmosferica. Poiche' i modelli non si estendono molto in acque profonde, hanno bisogno di informazioni aggiuntive sulle correnti al largo ed alla scarpata continentale.

I modelli costieri sono molto diversi ed hanno molte finalita' differenti, e implementazioni molto differenti. Molti modelli descritti precedentemente, inclusi i MOM e i MICOM, sono stati usati per modellare i processi costieri. Ma molti altri modelli specializzati sono stati sviluppati. Heaps (1987), Lynch et al., (1996), and Haidvogel (1998) forniscono una buona revisione sull'argomento. Piuttosto che passare in rivista tutti i modelli, parleremo di due tipologie di modello.

Princeton Ocean Model POM
Questo modello e' stato sviluppato da Blumberg e Mellor (1987) ed altri alla Princeton University ed alla Dynalysis di Princeton. E' largamente usato per descrivere le correnti costiere. Include i processi termodinamici, il mescolamento turbolento, e le approssimazioni di Boussinesq e idrostatica. Il parametro di Coriolis varia usando l'approssimazione del piano-beta. Poiche' il modello deve includere un vasto intervallo di profondita', Blumberg e Mellor usano coordinate verticali pesate con la profondita' dell'acqua:

(15.1)

dove z = h (x, y, t) e' la superfice marina, e z = - H (x, y) e' il fondo.

La turbolenza di sub-griglia e' parametrizzata usando uno schema di chiusura proposto da Mellor e Yamada (1982) dove i coefficienti di diffusione vorticosa variano con la misura dei vortici che producono il mescolamento e lo shear del flusso.

Il modello e' guidato dallo sforzo del vento e dai flussi di calore e dell'acqua dei modelli metereologici. Il modello usa la geostrofia, la marea, e le correnti di Eckman, conosciute al bordo esterno.

Il modello e' stato usato per calcolare la distribuzione tridimensionale della velocita', della salinita', della temperatura, della turbolenza e del livello marino per 30 giorni su una regione di 100-1000 km di lato con una griglia spaziata di 1-50 km.

Modello di Dartmouth Gulf of Maine
E' stato sviluppato da Lynch et al., (1996) e' un modello tridimensionale di circolazione che usa una griglia triangolare di elementi finiti. La misura dei triangoli e' proporzionale alla profondita' ed al tasso di cambiamento della profondita'. I triangoli sono piccoli nelle regioni dove la pendenza del fondo e' grande e dove la profondita' e' piccola, i triangoli sono grandi nelle acque profonde. La maglia variabile e' particolarmente utile nelle regioni costiere dove la profondita' dell'acqua varia molto. In questo modo la griglia variabile fornisce una risoluzione piu' alta dove c'e' piu' bisogno.

Il modello usa circa 13 000 triangoli per coprire il Golfo del Maine e le acque limitrofe del Nord Atlantico (Figura 15.3). La misura minima degli elementi e' circa un kilometro. Il modedllo ha da 10 a 40 strati orizzontali. La spaziatura verticale degli strati non e' uniforme.Gli strati sono piu' vicini tra loro all cima ed al fondo e sono piu' spaqziati all'interno. La spaziatura minima e' intorno al metro nello strato mescolato del fondo.

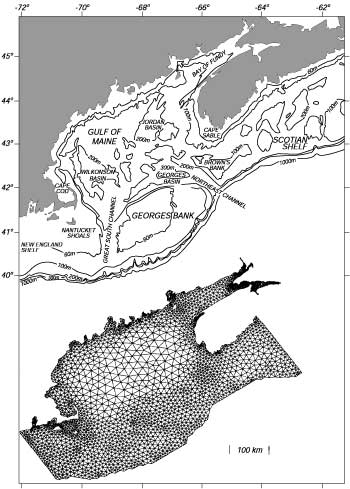Figura 15.3 Sopra: Mappa topografica del Golfo del Maine che mostra le caratteristiche piu' importanti. Sotto: La griglia triangolare, ad elementi finiti usata per calcolare la circolazione nel golfo. La grandezza dei triangoli varia con la profondita' ed il gradiente del fondale. Da Lynch et al. (1996).

Il modello integra le equazioni primitive, in tre dimensioni in acque poco profonde. Il modello ha una equazione di stato semplificata, una equazione di continuita' con profondita' mediata, e usa l'approssimazione idrostatica e quella di Boussinesq. Il mescolamento di sotto griglia del momento, del calore e di massa e' parametrizzato usando lo schema di chiusura della turbolenza di Mellor e Yamada (1982) che da' coefficienti di mescolamento verticale variabili con la stratificazione e lo shear di velocita'. I coefficienti di mescolamento orizzontali sono calcolati secondo Smagorinski (1963). Una viscosita' vorticosa scelta con cura e' usata nello strato limite del fondo. Il modello e' forzato con il vento, il riscaldamento, ed la forzante mareale del mare aperto.

Il modello e' inizializzato a riposo per pochi giorni usando un campo di densita' specifico in tutti i punti del grigliato, generalmente da unaq combinazione di dati di CTD e piu' i dati storici. Questo fornisce un campo di velocita' consistente con il campo di densita'. Il modello e' quindi forzato con i venti locali ed i flussi di calore per calcolare l'evoluzione dei campi di densita' e velocita'.

Commenti sui Modelli Costieri
Roed et al., (1995) esaminarono l'accuratezza dei modelli costieri comparando l'abilita' di cinque modelli, includendo il modello di Blumberg e Mellor per descrivere il flusso di casi tipici. Trovarono che i modelli producevano risultati molto differenti, ma che dopo che i modelli erano stati aggiustati, le differenze erano ridotte. Le differenze erano dovute al mescolamento verticale ed orizzontale ed alla risoluzione spaziale e temporale.

Hackett et al., (1995) compararono l' abilita' di due dei cinque modelli a descrivere il flusso sulla piattaforma norvegese. Concludendo che:

...entrambi i modelli sono capaci di generare qualitativamente molte delle caratteristiche osservate del flusso, ma nessuno e' capace di riprodurre quantitativamente le correnti. .. [Differenze] sono attribuibili principalmente alla parametrizzazione inadeguata del mescolamento turbolento a scala di subgriglia, alla mancanza di risoluzione orizzontale, ed alle imperfette condizioni iniziali e di contorno.

Modelli di 'Acqua Alta'
Le tempeste che si dirigono verso la costa, attraversando piattaforme continentali vaste e poco profonde, producono grandi variazioni del livello marino sulla costa, chiamate 'acque alte' (vedi §17.3 per una descrizione del sollevamento e dei processi collegati). I sollevamenti possono causare forti danni alle strutture costiere ed alla costa. Le forti tempeste del Golfo del Bengala hanno ucciso centinai di migliaia di persono in pochanno sviluppato modelli previsionali dei cambiamenti del livello giorni nel Bangladesh. Poiche' le 'acque alte' sono importanti, le agenzie governative in molti paesi hanno sviluppato modelli previsionali del cambiamento del livello marino e della estensione dell'allagamento costiero.

Questi calcoli non sono facili. Di seguito sono elencate alcune voci, in un vago ordine di importanza.

1. La distribuzione del vento sopra l'Oceano non e' ben conosciuta. i modelli numerici metereologici calcolano la velocita' del vento ad una superfice costante di pressione, i modelli di 'acqua alta' necessitano del vento ad una altezza fissa di 10 m. I venti nelle baie e nelle lagune tendono ad essere piu' deboli dei venti a largo perche' la terraferma vicina distorce il flusso dell'aria, e questo non e' incluso nei modelli metereologici.
2. La linea di costa del dominio del modello si estende verso terra con il tempo. Per esempio, se il livello sale, l'acqua sommerge la costa, ed il confine tra acqua e terraferma si muove verso l'interno, se il livello sale.
3. Il coefficiente dello sforzo del vento sull'acqua non e' ben conosciuto per la forza del vento di un uragano.
4. Il coefficiente dello sforzo dell'acqua sul fondo del mare non e' ben conosciuto.
5. I modelli devono includere le onde e le maree che influenzano il livello marino in acque poco profonde.
6. I modelli di 'acqua alta' devono includere le correnti generate dal vento in un mare stratificato e poco profondo.

Per ridurre gli errori, i modelli sono accordati per fornire i risultati che sono compatibili con le condizioni riscontrate nelle tempeste passate. Sfortunatamente, queste condizioni passate non sono ben conosciute. Le variazioni del livello marino e del vento sono raramente registrate accuratamente durante le tempeste eccetto in poche postazioni molto distanti fra loro. Tuttavia le altezze delle 'acque alte' possono variare di piu' di un metro su distanze di decine di kilometri.

A dispetto di tutti questi problemi, i modelli forniscono risultati molto utili. Guardiamo ad un modello comunemente usato.

Sea, Lake, and Overland Surges Model (SLOSH)
Questo modello e' usato dal NOAA per predirre le 'acque alte' prodotte dagli uragani che vengono verso terra lungo la costa statunitense dell'Atlantico e del Golfo del Messico (Jelesnianski, Chen, and Shaffer, 1992).

Il modello e' il risultato del lavoro di tutta la vita di Chester Jelesnianski. Nello sviluppo del modello, Jelesnianski e' stato molto attento alla importanza relativa degli errori nel modello. Egli lavoro' per ridurre gli errori piu' grandi e ignoro' quelli piccoli. Ad esempio , la distribuzione dei venti durante un uragano non e' ben conosciuta, cosi' non ha molto senso usare un coefficiente dello sforzo del vento variabile spazialmente. Tuttavia, Jelesnianski uso' un coefficiente dello sforzo costante nell'aria, ed un coefficiente costante dello sforzo vorticoso nell'acqua.

SLOSH calcola il livello marino dalle equazioni quasi lineari, in acqua poco profonda, integrate sulla profondita'. In questo modo, ignora la stratificazione. Ignora anche l'apporto fluviale, la pioggia e le maree. L'ultimo punto puo' sembrare strano, ma il modello e' progettato per le previsioni. Il tempo di quando arriva sulla costa non puo' essere predetto con precisione, e quindi l'altezza della marea e' sconosciuto. Le maree possono essere aggiunte al sollevamento calcolato, ma le interazioni non lineari della marea e dell'acqua alta sono ignorate.

Il modello e' forzato dai venti idealizzati dell'uragano. Ha solo bisogno della pressione atmosferica al centro della tempesta, la distanza dal centro all'area dei venti massimi, la previsione della traccia della tempesta e della velocita' lungo la traccia.

Per prevedere gli uragani che toccano terra vicino ad aree densamente popolate, il modello e' stato adattato per 27 zone dal porto di Boston Massachusetts alla Laguna Madre nel Texas. Il modello usa una maglia polare fissa. La spaziatura delle maglie comincia con una maglia piccola vicino il polo, che e' posiz ionato vicino alla citta' costiera per il quale il modello e' adattato. La griglia si allunga continuamente fino ad una maglia larga ai confini del modello di un grande bacino. Tale griglia fornisce una alta risoluzione nelle baie e vicino la costadove la risoluzione e' piu' necessaria. Usando le profondita' misurate in mare e le elevazioni in terra, il modello permette l'allagamento della terraferma, superando argini e dune, ed un flusso di sub-griglia attraverso i canali tra le isole.

I livelli marini calcolati dal modello sono stati comparati con le altezze misurate dai mareografi per 13 tempeste, includendo Betsy (1965), Camile (1969), Donna (1960), e Carla (1961). l'accuratezza risultante e' stata di ± 20%.

Advanced Circulation Model ADCIRC
Questo e' un modello sperimentale per prevedere le 'acque alte' prodotte dagli uragani che vengono in terra lungo le coste dell'Atlantico e le coste del Golfo degli Stati Uniti (Graber et al, 2006). Il modello usa una griglia agli elementi finiti, l'approssimazione di Boussinesq, un attrito sul fondo quadratico, e le equazioni di continuita' e del momento per un flusso su una terra rotante, integrate verticalmente. Puo' girare sia in due dimensioni, integrate nella profondita', o come modello tridimensionale. Poiche' le onde contribuiscono all'acqua alta, il modello include le onde calcolate dal modello di terza generazione per le onde WAM (vedi §16.5).

Il modello e' forzato da:

1. I venti e la pressione superficiale ad alta risoluzione ottenuta dal combinare le previsioni del tempo dal NOAA National Weather Service e dal National Hurricane Center lungo la traccia prevista ufficiale e alternativa della tempesta.
2. Le maree ai confini di mare aperto del modello.
3. L'altezza della superfice marina e le correnti al confine di mare aperto del modello.

Il modello predisse con successo l'acqua alta dell'uragano Katrina, dando valori di 6.1 m vicino New Orleans.

15.5 Modelli di Assimilazione

Molti modelli che abbiamo descritto finora hanno come output la velocita' della corrente o la topografia della superfice marina, che sono pero' vincolate dalle osservazioni oceanografiche delle variabili che i modelli calcolano. Tali modelli sono detti modelli di assimilazione. In questa sezione, consideriamo come i data possono essere assimilati dentro i modelli numerici.

Cominciamo con i modelli numerici alle equazioni primitive, che ammettono i vortici per calcolare la posizione della Gulf Stream. Assumiamo che il modello e' forzato con i venti reali di superfice del modello atmosferico ECMWF. Usando il modello, possiamo calcolare la posizione della corrente ed anche la topografia della superfice marina associata alla corrente. Troviamo che la posizione della Gulf Stream comincia ad ondeggiare a largo di Capo Hatteras a causa dell instabilita', e la posizione calcolata dal modello e' solo una delle tante possibili posizioni per la stesso vento forzante. Quale e' la posizione corretta, cioe', qual'e' la posizione della corrente attuale? Sappiamo, dal satellite altimetrico, la posizione della corrente in alcuni punti ad alcuni giorni fa'. Possiamo usare queste informazioni per calcolare la posizione odierna della currente? Come dobbiamo assimilare queste informazioni dentro il modello?

Molti approcci differenti sono stati provati (Malanotte-Rizzoli, 1996). Roger Daley (1991) fornisce una descrizione completa di come sono usati i dati nei modelli atmosferici. Andrew Bennet (1992) e Carl Wunsch (1996) descrivono le applicazioni oceaniche.

L'assimilazione dei dati dentro i modelli non e' facile.

1. L'assimilazione dei dati e' un problema inverso (inverse problem): Un numero finito di osservazioni sono usate per stimare un campo continuo - una funzione, che ha un numero infinito di punti. I campi calcolati, la soluzione al problema inverso, sono completamente sotto determinati. Ci sono molti campi che si adattano alle osservazioni ed al modello con precisione, e le soluzioni non sono uniche. Nel nostro esempio, la posizione della Gulf Stream e' una funzione. Possiamo non aver bisogno di un numero infinito di valori per specificare la posizione della corrente se assumiamo che la positione e' qualcosa di approssimato nello spazio. Ma certamente necessitiamo di centinaia di valori lungo l'asse della corrente. Inoltre, disponiamo di pochi punti dei satelliti per vincolare la posizione della corrente.
   Per saperne di piu' sul problema inverso e la sua soluzione ,vedi Parker (1994) che fornisce una introduzione molto buona basata su esempi geofisici.
2. La dinamica dell'Oceano non e' lineare, mentre la maggior parte dei metodi per calcolare le soluzioni al problema inverso dipende da approssimazioni lineari. Per esempio la posizione della Gulf Stream e' una funzione molto non-lineare della forzante del vento e dei flussi di calore nel Nord Atlantico.
3. Sia il model che i dati sono incompleti ed entrambi hanno errori. Per esempio, abbiamo misure altimetriche soltanto lungo le tracce mostrate nella Figura 2.6, e le misure hanno errori di ± 4cm.
4. La maggior parte dei dati disponibili per l'assimilatione proviene dai dati superficiali, come i dati AVHRR e quelli altimetrici. Ovviamente i dati di superfice vincolano le velocita' geostrofiche superficiali, che sono collegate a quelle piu' profonde. Il trucco e' di accoppiare le osservazione di superfice alle correnti profonde.

Varie tecniche sono state usate per vincolare i modelli numerici in oceanografia, forse i piu' pratici sono le tecniche derivate dalla meteorologia.

Le piu' importanti correnti oceaniche hanno dinamiche che sono molto non lineari. Questo preclude un rapido sviluppo del metodo inverso. Percio', I principali tentativi di combinare i modelli oceanici con le misure hanno seguito le procedure usate nella meteorologia operativa: le osservazioni sono usate per preparare le condizioni iniziali del model, che e' quindi integrato nel tempo fino a quando ulteriori misure sono disponibili. Il modello e' subito ri-inizializzato. Questa strategia puo' essere descritta come sequenziale.
Da Bennet (1992).

Vediamo adesso, come il Professore Allan Robinson e colleghi alla Harvard University Hanno usato le tecniche sequenziali di stima per prevedere la posizione della Gulf Stream.

Harvard Open-Ocean Model
Questo e' un modello quasi-geostrofico per la Gulf Stream ad est di Capo Hatteras che ammette vortici (Robinson et al. 1989). Ha sei livelli nella verticale, 15 km di risoluzione, e mezz'ora di passo temporale. Usa un filtro semplice per abbassare la variabilita' di alta frequenza e per smorzare la variabilita' a scala di griglia.

Per quasi-geostrofico voglio dire che il campo del flusso e' chiuso dal bilancio geostrofico. Le equazioni del moto includono i termini dell'accelerazione D /Dt , dove D /Dt e' la derivata totale e t e' il tempo. Il flusso puo' essere stratificato, ma non c'e' cambiamento nella densita' dovuto ai flussi di calore oppure al mescolamento verticale. In questo modo le equazioni quasii-geostrofiche sono piu' semplici delle equazioni primitive, e possono essere integrate molto piu' velocemente. Cushman-Roisin (1994: 204) forniscono una buona descrizione dello sviluppo delle equazioni del moto quasi-geostrofiche.

Il modello riproduce le caratteristiche importanti della Gulf Stream e della sua estensione, includendo meandri, vortici a nucleo freddo e caldo, le interazioni dei vortici con la corrente, e le instabilita' barocline. Poiche' il modello e' stato progettato per prevedere la dinamica della Gulf Stream, deve essere vincolato dalle misure oceanografiche:

1. I dati forniscono le condizioni inziali del modello. Le misure da satellite della temperatura superficiale dal AVHRR e la topografia dagli altimetri sono usate per determinare la posizione delle caratteristiche nella regione. Le misure di XBT, AXBT della temperatura sotto la superfice, e le misure storiche della densita' interna sono usate. Le caratteristiche sono rappresentate da semplici funzioni analitiche nel modello.
2. I dati sono introdotti nel modello numerico, che interpola e arrotonda i dati per produrre la migliore stima dei campi iniziali di densita' e velocita'. I campi risultanti sono chiamati analisi.
3. Il modello e' integrated in avanti per una settimana, fino a quando sono disponibili i nuovi dati, per produrre una previsione.
4. Finalmente, i nuovi dati sono introdotti nel modello come nel primo passo qui sopra, ed il processo e' ripetuto.

Il modello e' stato usato per fare con successo previsioni fino ad una settimana della Gulf Stream e della regione (Figura 15.4).

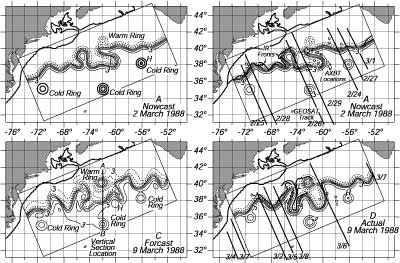Figura 15.4 Output del modello di Harvard Open-Ocean Model: A lo stato iniziale del modello, l'analisi, e B i dati usati per produrre l'analisi del 2 marzo 1988. C La previsione per il 9 marzo 1988. D l'analisi del 9 marzo. Sebbene la Gulf Stream canbia sostanzialmente in una settimana, il modello modello prevede bene le variazioni. Da Robinson et al. (1989).

Molti modelli piu' avanzati con risoluzione molto piu' alta sono stati usati per fare previsioni globali delle correnti oceaniche fino ad un mese di anticipo in sostegno dell'esperimento del Global Ocean Data Assimilation Experiment (GODAE) che e' cominciato nel 2003. Lo scopo del GODAE e' di produrre previsioni oceaniche di routine simili alle attuali previsioni del tempo.

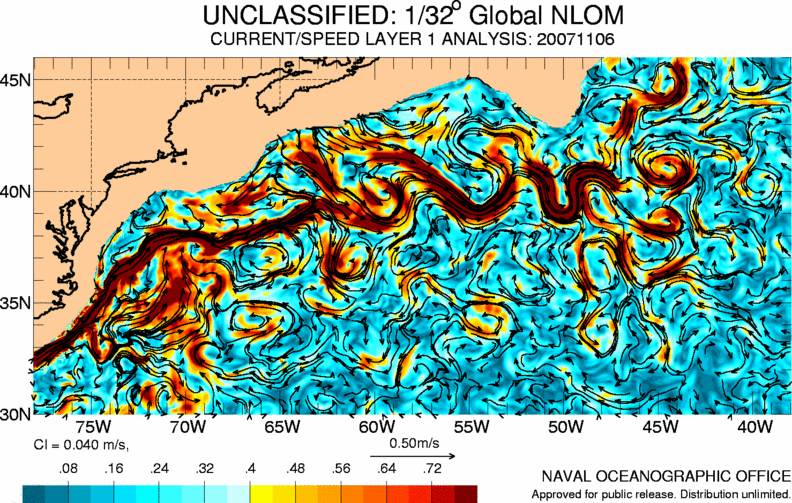
Navy Layered Ocean Model
Un esempio di modello GODAE e' il modello US Navy Layered Ocean. E' un modello alle equazioni primitive con una risoluzione di 1/32° in orizzontale e sette strati in verticale. Assimila i dati altimetrici dai satelliti Jason, Geosat Follow-on GFO, ed ERS-2, le temperature superficiali del mare dai AVHRR sui satelliti del NOAA. Il modello e' forzato con i venti ed i flussi del calore fino a cinque giorni nel futuro usando le output dal Navy Operational Global Atmospheric Prediction System. Oltre i cinque giorni, sono usate le medie stagionali dei venti e dei flussi. Il modello gira giornalmente e produce previsioni fino ad un mese nel futuro. La previsione e' buona fino a venti giorni.

Correnti oceaniche superficiali calcolate dal modello US Navy Layered Ocean Model per la regione della Gulf Stream del 6 novembre 2007.

Un gruppo di laboratori e agenzie francesi usa un sistema simile di previsioni operative, Mercator, basato sull'assimilazione di misure altimetriche delle altezze della superfice marina, misure satellitari della temperatura superficiale e dei campi di densita' interni all'oceano e correnti a 1000 m da migliaia di sonde alla deriva Argo. Il loro modello ha una risoluzione di 1/15° nell'Atlantico e di 2° globalmente.

15.6 Modelli accoppiati Oceano-Atmosfera

I modelli numerici accoppiati dell'atmosfera e dell'oceano sono usati per studiare il sistema climatico, la sua variabilita' naturale, e la risposta alle forzanti esterne. L'uso piu' importante e' stato di studiare come il clima terrestre puo' rispondere al raddoppiamento della quantita' di CO₂ nell'atmosfera. Molta della letteratura sul cambiamento climatico e' basata sugli studi che usano tali modelli. Gli altri usi importanti dei modelli accoppiati includono gli studi del El Niño e della circolazione della controcorrente lungo i meridiani. I primi variano su periodi di pochi anni, gli ultimi su periodi di pochi secoli .

Lo sviluppo del lavoro e' sempre piu' coordinato attraverso il World Climate Research Program del World Meteorological Organization WCRP/WMO, ed i recenti progressi sono riassunti nel capitolo 8 del Climate Change 2001: The Scientific Basis un rapporto del Intergovernmental Panel on Climate Change (McAvaney, et al, 2001).

Molti modelli accoppiati oceano-atmosfera sono stati sviluppati. Alcuni includono soltanto processi fisici nell'oceano, nell'atmosfera e nelle regiono polari coperte dal ghiaccio. Altri aggiungono l'influenza della terraferma e dell'attivita' biologica nell'oceano. Vediamo la componente oceanica di alcuni modelli.

Modello del Sistema Climatico
Il modello del sistema climatico sviluppato dal Centro Nazionale per le Ricerche Atmosferiche (NCAR) include l'influenza fisica e biogeochimica sul sistema del clima (Boville e Gent, 1998). Il modello ha le componenti dell'atmosfera, dell'Oceano, della terraferma superficiale, e del ghiaccio marino accoppiati dai flussi tra quest componenti. La componente atmosferica e' il modello dell'NCAR: Community Climate Model, la componente oceanica e' una versione modificata del modello di Oceano Modulare di Princeton, che usa lo schema di Gent e McWilliams (1990) per parametrizzare i vortici d mesoscala. La risoluzione e' di circa 2° × 2° con 45 livelli verticali nell'Oceano.

Il modello e' stato provato (spin up) ed integrato per 300 anni, i risultati sono realistici, e non c'e' bisogno di un aggiustamento del flusso. (Vedi il numero speciale del Journal of Climate, Giugno 1998).

Modello Accoppiato di Princeton
Il modello consiste di un modello atmosferico con una risoluzione orizzontale di 7.5° in longitudine e di 4.5° in latitudine con 9 livelli in verticale, un modello oceanico con una risoluzione orizzontale 4° e 12 livelli in verticale, ed un modello per la superfice della terraferma. L'Oceano e l'atmosfera sono accoppiati attraverso i flussi di calore, di acqua e di momento. La terraferma e l'Oceano sono accoppiati attraverso il flusso di acqua dei fiumi. E la terraferma e l'Atmosfera attraverso i flussi di acqua e calore.

Il Modello del Centro di Hadley
Questo e' un modello atmosfera-oceano-ghiacci che minimizza la necessita' degli aggiustamenti nei flussi (Johns et al, 1997). La componente dell'Oceano e' basata sul modello alle equazioni primitive di Bryan-Cox, con fond realistico, coefficienti di mescolamento verticaleda Pacanowski e Philander (1981). La componente dell'oceano e dell'atmosfera hanno entrambe una risoluzione orizzontale 96 × 73 punti di griglia, l'oceano ha 20 livelli nella verticale.

In contrasto a molti modelli accoppiati, questo e' inizializzato come sistema accoppiato con aggiustamenti dei flussi durante lo spin up per mantenere la temperature e la salinita' della superfice marina vicina ai valori medi osservati. Il modello accoppiato e' successivamente integrato usando i valori di Levitus con le temperature e salinita' di settembre. L'integrazione iniziale va' dal 1850 al 1940. Il modello e' stato poi integrato per altri 1000 anni. Non sono stati necessari aggiustamenti dei flussi nei primi 140 anni di integrazione perche' la deriva della temperatura media globale dell'aria e' stata di ≤ 0.016 K/secolo.

Commenti sull'Accuratezza dei Modelli Accoppiati
I modelli del sistema climatico terra-aria-ghiaccio-oceano devono, ancora, simulare centinaia di migliaia di anni.

Sara' molto difficile stabilire un quadro di integrazione, particolarmente su scala globale, con le attuali capacita' piuttosto limitate per modellare il sistema della Terra. Un doppio approccio e' stato progettato. Da una parte, l'approccio relativamente convenzionale di migliorare i modelli accoppiati atmosfera-oceano-terra-ghiaccio sara' perseguito. Ingegnosita' a parte, lo sforzo di calcolo e' immenso, cos'i e' stato creato il Simulatore del Sistema Terra (Earth System Simulator) - 640 super-computer collegati per fornire 40 teraflop [10¹² operazioni in virgola mobile al secondo ed un sistema di raffreddamento sul piano sottostante - che e' in costruzione in Giappone dal 2003. From Newton (1999).

Poiche' i modelli devono essere semplificati per girare sugli attuali computer, i modelli devono essere piu' semplici di quelli che simulano la circolazione per pochi anni (WCRP, 1995).

Inoltre, imodelli accoppiati devono essere integrati per molti anni prima che l'oceano e l'atmosfera raggiungano un equilibrio. Come l'integrazione procede, il sistema accoppiato tende a derivare lontano dalla realta' a causa di errori nel calcolo dei flussi di calore e del momento tra l'oceano e l'atmosfera. Per esempio, errori molto piccoli nelle precipitazioni oltre il Circolo Polare Aantartico porta a piccole variazioni della corrente, che creano grande variazioni nella convezione profonda nel mare di Weddell, che influenzano pesantemente il volume delle masse di acqua profonde.

Alcuni modellisti permettono al sistema di derivare, altri aggiustano la temperatura superficiale ed i flussi calcolati tra oceano e atmosfera. Ritornando agli esempi, il flusso di acqua dolce nella corrente circumpolare potrebbe essere aggiustata mantendo la salinita vicina al valore osservato nella corrente. Non c'e' una base scientifica buona per gli aggiustamenti, eccetto il desiderio di produrre un "buon" modello accoppiato. Quindi, gli aggiustamenti sono "ad hoc" e discutibili. Tali aggiustamenti sono chiamati: aggiustamenti del flusso oppure correzioni del flusso.

Fortunatamente, i modelli sono continuamente migliorati, il bisogno degli aggiustamenti o la grandezza dell'aggiustamento sono sempre piu' ridotti. Per esempio, usando lo schema di Gent-McWilliams per il mescolamento lungo le superfici di densita' costante in un modello accoppiato oceano-atmosfera la deriva del clima e' fortemente ridotta perche' lo schema di mescolamento riduce la convezione profonda nella Corrente Circumpolare Antartica ed altrove (Hirst, O'Farrell, e Gordon, 2000).

Grassl (2000) elenca le quattro caratteristiche di un modello di circolazione generale accoppiato credibile:

1. Adeguata rappresentazione del clima attuale.
2. Riproduzione (dentro variazioni climatiche interannuali ed a scala temporale di decenni) dei cambiamenti delle forzanti esterne fin dall'inizio delle registrazioni strumentali per una data storia.
3. Riproduzione di un episodio climatico differente del passato come descritto dalle registrazioni paleo-climatiche....
   for given estimates of the history of external forcing; and
4. Simulare con successo le caratteristiche piu' importanti di una variazione climatica violenta del passato.

McAvaney et al. (2001) hanno comparato la componente oceanica di ventiquattro modelli accoppiati, includendo quelli con e senza aggiustamento dei flussi. Hanno trovato sostanziali differenze tra i modelli. Ad esempio, solo cinque modelli calcolano una circolazione rovesciata lungo i meridiani entro 10% del valore osservato di 20 Sv. Alcuni hanno valori bassi comi 3 Sv, altri alti come 36 Sv. La maggior parte dei modelli non calcola un trasporto realistico della Corrente Circumpolare Antartica.

Grassl (2000), quattro anni piu' tardi, ha trovato che molti modelli, includendo quelli con e senza aggiustamenti dei flussi, aderiscono al primo criterio.Alcuni modelli soddisfano il secondo, ma la forzante solare esterna non e' ancora ben conosciuta e necessita di apltro lavoro. Solo pochi modelli stanno incominciando a riprodurre alcuni aspetti dell'evento caldo di 6,000 anni fa'.

Ma che utilita' hanno questi modelli nel fare proiezioni del clima futuro? Le opinioni sono polarizzate. Ad un estremo ci sono quelli che vedono i risultati del modello come Vangelo. Dall'altra parte ci sono quelli che denigrano i risultati semplicemente perche' non credono nei modelli, oppure piu' semplicemente, che i risultati dei modelli sono sbagliati in alcuni aspetti, e che alcuni processi non sono stati inclusi adeguatamente. La verita' e' nel mezzo. Tutti i modelli sono certamente in errore, perche' , per progetto, tutti devono riprodurre una visione semplificata del sistema che stanno modellando. Tuttavia, molti - ma non tutti - modelli sono molto utili.
Da Trenberth (1997).

15.7 Concetti Importanti

1. I modelli numerici sono usati per simulare i flussi dell'Oceano con risultati utili e realistici. I modelli piu' recenti includono i flussi del calore attraverso la superfice, la forzante del vento, i vortici di mesoscala, le coste realistiche, le caratteristiche reali del fondo marino, e piu' di 20 livelli in verticale.
   
2. I modelli recenti sono cosi' efficaci, che con una risoluzione vicina al 0.1°, mostrano aspetti precedentemente sconosciuti della circolazione oceanica.
   
3. I modelli numerici non sono perfetti. Risolvono equazioni discrete, che non sono esattamente le equazioni del moto descritte nei precedenti capitoli.
   
4. I modelli numerici non possono riprodurre tutta la turbolenza dell'Oceano perche' la griglia dei punti sono separate dalle decine alle centinaia di kilometri. L'influenza del moto turbolento sulle piccole distanze deve essere calcolato dalla teoria, e questo introduce degli errori.
   
5. I modelli numerici possono essere forzati dai dati oceanografici delle navi e dei satelliti in tempo reale per produrre previsioni delle condizioni oceanografiche, che includono la condizione di El Niño nel Pacifico, e la posizione della Corrente del Golfo in Atlantico.
   
6. I modelli accoppiati oceano-atmosfera hanno una risoluzione molto piu' bassa e possono essere integrati per centinaia di anni per simulare la variabilita' naturale del sistema climatico e la sua risposta all'aumento della CO₂ nell'atmosfera.