Capitolo 17 - Processi Costieri e Marea

Nell'ultimo Capitolo ho discusso sulle onde alla superfice del mare. Ora possiamo considerare molti casi importanti e speciali: la transformazione delle onde quando arrivano sulla spiaggia e si rompono; le correnti e le onde di bordo generate dall'interazione delle onde con le coste; i maremoti; le 'acque alte' e le maree, specialmente le maree lungo le coste.

17.1 Onde di Costa e Processi Costieri

Le velocita' di fase e di gruppo delle onde sono in funzione delle profondita' quando questa e' inferiore ad un quarto della lunghezza d'onda in acque profonde. Il periodo e quindi la frequenza sono invarianti (non cambiano come l'onda si avvicina alla spiaggia); e questo e' usato per calcolare le propieta' delle onde costiere. L'altezza dell'onda aumenta quando la velocita' di gruppo dell'onda rallenta. La lunghezza dell'onda diminuisce. Le onde cambiano direzione a causa della rifrazione. Infine, le onde si rompono se l'acqua e' sufficientemente poco profonda; e le onde rotte portano acqua nella zona di surf, creando correnti lungo la costa ed attraverso.

Onde Costiere
La relazione di dispersione (16.3) e' usata per calcolare le propieta' delle onde quando queste si propagano da acque profonde al largo ad acque basse poco prima della zona di surf. Poiche' la (16.3) rimane constante, abbiamo:

(17.1)

dove

(17.2)

e L e' la lunghezza d'onda, c e' la velocita' di fase, α e' l'angolo della cresta relativo alla linea di profondita' constante, e d e' la profondita'. L'indice 0 sottoscritto indica i valori in acque profonde.

La quantita' d / L e' calcolata dalla soluzione di

(17.3)

usando una tecnica iterative, o dalla Figura 17.1 oppure dalla tabella A1 di Wiegel (1964).

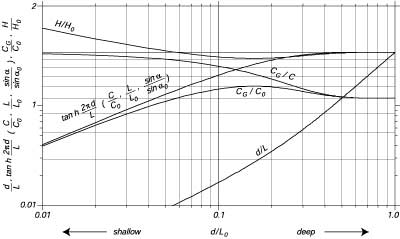Figura 17.1 Cambio nelle propieta' delle onde quando le onde si avvicinano alla costa. Da Wiegel (1964).

Poiche' la velocita' delle onde e' una funzione della profondita' in acque poco profonde, le variazioni della profondita' a largo possono focalizzare o defocalizzare l'energia delle onde che raggiungono la riva. Consideriamo il semplice caso di onde con creste da acqua profonda parallele ad una costa dritta con due promontori, che si estendono verso il mare (Figura 17.2). La velocita' di gruppo delle onde e' piu' veloce nelle acque piu' profonde tra i due promontori, e le creste delle onde diventano progressivamente deformate quandol'onda si propaga verso la spiaggia. L'energia dell'onda, che si propaga perpendicolarmente alla cresta dell'onda, e' rifratta nella regione tra i due promontori. Quindi accade, che l'energia dell'onda e' focalizzata sulle punte dei promontori, e la rottura li' e' molto piu' forte di quelle nalla baia. La differenza in altezza d'onda puo' essere sorprendentemente grande. In un giorno calmo, le rotture possono essere alte 60 cm sopra un canion sottomarino alla spiaggia di La Jolla, San Diego California, poco a sud dello Scripps Institution of Oceanography. Allo stesso tempo, le onde poco a nord del canyon possono essere alte abbastanza da attirare i surfisti.

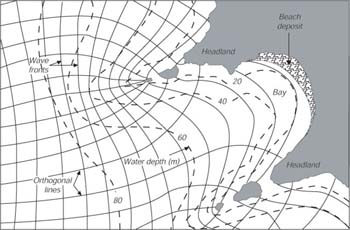Figura 17.2 Le forme sottomarine, come i canyon e le piccole colline, al largo della costa possono infuenzare molto il punto di rottura a valle della forma. Da Thurman (1985).

Onde che si rompono
Come le onde si muovono verso acque poco profonde, La velocita' di gruppo diventa piccola, l'energia delle onde per metro quadro aumenta, ed i termini non lineari nelle equazioni delle onde diventano importanti. Questi processi causano onde piu' alte, con creste scoscese e cavi piu' profondi. Quando la pendenza alla cresta diventa sufficientemente ripida, l'onda si rompe (Figura 17.3 Sinistra). La forma dell'onda che si rompe dipende dalla pendenza del fondo, e dall'inclinazione dell'onda a largo (Figura 17.3 Destra).

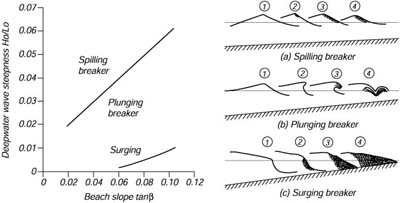Figura 17.3 Sinistra: Classificazione delle onde che si rompono in funzione della pendenza del fondo e dell'inclinazione dell'onda al largo. Destra: Schema dei tipi di rotture di onde. Da Horikawa (1988).

1. Le onde ripide tendono a perdere energia lentamente quando, muovendosi verso acque meno profonde, l'acqua cade giu' dal fronte dell'onda. Queste sono le 'spilling breakers' : frangenti cadenti.
2. Onde meno ripide su spiagge scoscese tendono ad inclinarsi cosi' rapidamente che la cresta dell'onda si muove piu' velocemente del cavo, e la cresta, correndo in avanti, si tuffa nel cavo (Figura 17.4) 'plunging breakers' : frangenti tuffanti.
3. Se la spiaggia e' sufficientemente ripida, l'onda puo' sollevarsi fino alla fine senza rompersi nel senso che si formi la schiuma. O se si forma, e' solo sulla parte che risale la spiaggia. Un esempio estremo dovrebbe essere un'onda incidente su una diga verticale 'surging breakers' : frangenti alzanti.

Figura 17.4 Frangenti ripidi a tuffo sono l'arche-tipo dei frangenti. I bordo di tali frangenti sono ideali per il surf. Foto di Jeff Devine.

Correnti prodotte dalle Onde
Le onde si rompono in una fascia stretta di acqua poco profonda lung la spiaggia, la zona di surf. Dopo la rottura, l'onda continua come un muro quasi verticale di acqua turbolenta chiamata onda solitaria (bore) che trasporta l'acqua fino alla spiaggia. Dapprima, l'onda risale la spiaggia quindi si ritira. L'acqua portata dall'onda rotta e' lasciata nelle acque basse dietro la zona di rottura.

L'acqua scaricata dentro la zona di rottura deve ritornare al largo. Fa' questo prima muovendosi parallela alla spiaggia come una corrente lungo la spiaggia. Poi gira e fluisce verso il largo perpendicolare alla spiaggia in un corrente stretta, veloce la corrente di risucchio. Queste correnti sono di solito distanti centinaia di metri una dall'altra (Figura 17.5). Generalmente c'e' una fascia di acqua piu' profonda tra la zona di rottura e la spiaggia, le correnti lungo la spiaggia corrono in questi canali. La forza di una corrente di risucchio dipende dall'altezza e dalla frequenza delle onde che si rompono, e dalla forza del vento verso la spiaggia. Le correnti di risucchio sono un pericolo per i bagnanti sprovveduti, specialmente i nuotatori meno bravi che sono dentro la zona di rottura, sono portati lungo la spiaggia dalle correnti fino a che sono trascinati improvvisamente al largo dalla corrente di risucchio. Nuotare contro il risucchio e' inutile, ma si puo' scappare nuotando parallelo alla spiaggia.

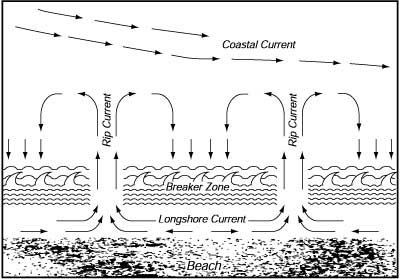Figura 17.5 Schema di correnti trasversali generate dall'acqua portata verso la spiaggia dalle onde che si rompono. Da Dietrich, Kalle, Krauss, & Siedler (1980).

Onde di Bordo sono prodotte dalla variabilita' dell'energia delle onde che raggiungono la riva. Le onde tendono a muoversi in gruppi, specialmente quando le onde provengono da tempeste lontane. Per molti minuti le onde che si rompono possono essere piu' piccole della media, Poi poche onde grandi si romperanno. Le variazioni nell'altezza delle rotture minuto -per- minuto producono variabilita' di bassa frequenza nelle correnti lungo la costa. Questo, crea un'onda di bassa frequenza attaccata alla spiaggia, un onda di bordo. Le onde hanno periodi di pochi minuti, un lunghezza d'onda di circa un kilometro, ed un'ampiezza che decade esponenzialmente verso il largo (Figura 17.6).

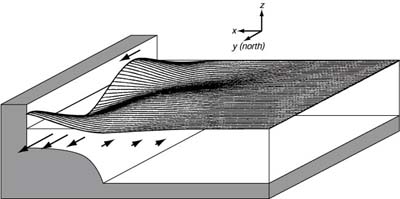Figura 17.6 Schema disegnato con il computer di una onda di bordo. Tali onde esistono nella zona di rottura vicino la spiaggia e lungo la piattaforma continentale. Da Cutchin e Smith (1973).

17.2 Maremoto (Tsunami)

Gli tsunami sono onde oceaniche di bassa frequenza generate dai terremoti sottomarini. L'improvviso movimento del fondo marino su distanze di un centinaio di kilometri genera onde con un periodo di circa 12 minuti (Figura 17.7). Un veloce conto mostra che oggetti devono essere onde di acqua bassa, che si propagano ad una velocita' di 180 m/s ed hanno una lunghezza d'onda di130 km in acqua profonda 3.6 km (Figura 17.8). Le onde non sono riconoscibili in alto mare, ma quando si avvicinano alla costa, e dopo la rifrazione con oggetti sommersi, possono venire alla spiaggia e alzarsi ad altezze di dieci e piu' metri sopra il livello del mare. In un esempio estremo, Uno tsunami in Alaska il 1 aprile 1946 distrusse il faro di Capo Scotch posto a 31m sopra il livello del mare.

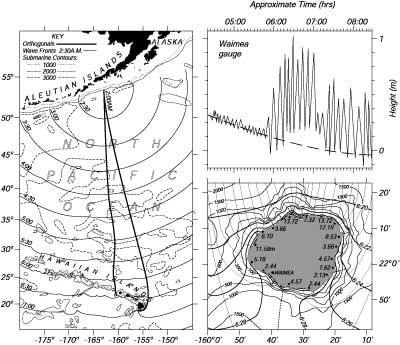Figura 17.7 (Sinistra)Posizioni orarie delle onde primarie dello tsunami generato da un grande terremoto nella Fossa delle Aleutine il 1Aprile 1946 alle 12:59 GMT. (Destra alto) Livello del mare registrato nell'estuario del fiume Waimea (Destra basso) Mappa dell'isola di Kauai che mostra le altezze raggiunte dall'acqua (in metri sopra la LLW) durante lo tsunami, i fronti dell'onda, gli ortogonali ed i contorni del fondo marino. I tempi riportano il tempo calcolato di arrivo della prima onda. Da Shepard, McDonald e Cox (1950).

Figura 17.8 Altezza dell'onda di tsunami quattro ore dopo il grande terremoto M9 Cascadia a largo dello stato di Washington il 26 gennaio 1700 calcolato con un modello numerico ad elementi finiti. L'altezza d'onda massima in oceano aperto, e' di circa un metro, a nord delle Hawaii. Da Satake et al. (1996).

Shepard (1963, Capitolo 4) riassume l'influenza degli tsunami basata sui suoi studi nel Pacifico.

1. Gli tsunami sembrano essere prodotti dal movimento (un terremoto) lungo una faglia lineare.
2. Gli tsunami possono viaggiare per migliaia di kilometri e fare ancora molto danno.
3. La prima onda dello tsunami non sembra essere la piu' grande.
4. Le ampiezze dell'onda sono relativamente grandi di fronte a montagne sottomarine. Relativamente basse di fronte alle valli, a patto che queste caratteristiche si trovino in acque profonde.
5. Le ampiezze delle onde descrescono in presenza di barriere coralline che proteggono la costa.
6. Alcune baie hanno un effetto amplificatore, ma gli estuari lunghi attenuano le onde.
7. Le onde possono passare intorno a isole circolari senza grossa perdita di energia, ma sono attenuate nei lati sottovento di isole allungate ed angolari.

17.3 Acqua Alta (Storm Surge)

I venti di tempesta che soffiano sulle piattaforme continentali poco profonde sollevano l'acqua contro la costa. L'aumento del livello marino e' conosciuto come 'acqua alta'. Molti processi sono importanti:

1. Il trasporto di Ekman con venti paralleli alla costa spingono l'acqua verso la costa causando un sollevamento del livello marino.
2. I venti che soffiano verso la costa spingono l'acqua direttamente verso la costa.
3. Le onde che si muovono e le interazioni con altre onde transportano acqua verso la costa aggiungendosi ai primi due processi.
4. Le onde di bordo generate dal vento che viaggiano lungo la costa.
5. La bassa pressione atmosferica della tempesta alza il livello marino di un centimetro per ogni millibar di pressione in meno, attraverso l'effetto del barometro invertito.
6. Per finire, l'acqua alta' si aggiunge alle maree, e le alte maree possono cambiare una rimonta relativamente debole in una molto piu' pericolosa.

Vedere Jelesnianski (1967, 1970) e §15.5 per la descrizione del modello di storm-surge SPLASH e Mare, Lago, e Overland Surges dal Hurricanes SLOSH usato dal National Hurricane Center e §15.5.

Per una prima a approssimazione rozza, il vento che soffia su un acque poco profonde produce una pendenza della superfice marina proporzionale allo sforzo del vento.

(17.4)

dove ζ e' il livello marino, x e' la distanza orizzontale, H e' la profondita' dell'acqua, T₀ e' lo sforzo del vento alla superfice del mare, ρ e' la densita' dell'acqua; e g e' l'accelerazione gravitazionale.

Se x = 100 km, U = 40 m/s, e H = 20 m, i valori tipici di un uragano al largo della costa del Golfo del Texas, allora ζ = 2.7 Pa, e z = 1. 3 m alla spiaggia. La Figura 17.9 mostra la frequenza delle rimonte in Olanda ed un metodo grafico per stimare la probabilita' di eventi estremi usando la probabilita' di eventi deboli.

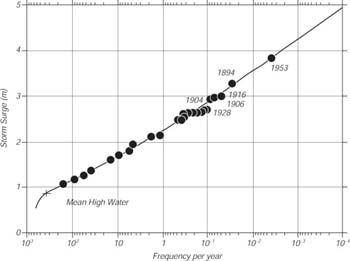Figura 17.9 Distribuzione della densita' di probalita' (per anno) delle altezze verticali di 'acque alte' in Olanda. La funzione di distribuzione e' di Rayleigh, e la probabilita' di grandi rimonte puo' essere stimata dall'estrapolare la probabilita' osservata di rimonte piu' piccole e piu' comuni. Da Wiegel (1964).

17.4 La Teoria della Marea

La Marea e' stata cosi' importante per il commercio e la scienza per cosi' tanti migliaia di anni che la marea e' enterata nel nostro linguaggio quotidiano: time and tide wait for no one, the ebb and flow of events, a high-water mark, e turn the tide of battle.

1. La Marea produce forti correnti in molte parti del mondo. Le correnti di marea possono avere fino a 5 m/s nelle acque costiere, impedendo la navigazione e mescolando le acque costiere.
2. Le correnti di Marea generano onde interne sopra le montagne sommerse, lungo le scarpate continentali e nelle dorsali medie-oceaniche. Le onde dissipano l'energia mareale. La rottura delle onde interne e le correnti mareali sono le maggiori forze che producono il mescolamento oceanico profondo.
3. Le correnti di Marea possono risospendere i sedimenti del fondo, anche nell'oceano profondo.
4. La crosta della Terra e' elastica. Si flette sotto l'influenza del potenziale mareale. Si flette anche sotto il peso delle maree oceaniche. Con il risultato, che il fondo marino e i continentiin risposta alle maree si muovono su e giu' di circa 10 cm. La deformazione della Terraferma influenza tutte le misure geodetiche precise.
5. La Marea dell'Oceano e' in ritardo rispetto al potenziale che genera la marea. Questo produce forze che trasferiscono momento angolare tra la Terra ed il corpo che produce la marea, specialmente la Luna. Come risultato delle forze di marea, la rotazione della Terra rispetto al suo asse rallenta, causando un lento allontanamento della Luna, e causando un rallentamento della rotazione della Luna rispetto al suo asse, che forza la Luna a mantenere lo stesso lato che guarda la Terra anche se la Luna ruota intorno alla Terra.
6. La Marea influenza le orbite dei satelliti. La conoscenza accurata della Marea e' necessaria per calcolare le orbite dei satelliti altimetrici e per correggere le misure oceaniche degli altimetri.topografia.
7. Le forze di Marea sugli altri pianeti e sulle stelle sono importanti per la comprensione di molti aspetti della dinamica del sistema solare e perfino nella dinamica delle galassie. Per esempio, la velocita' di rotazione di Mercurio, di Venere, e di Io derivano dalle forze di marea.

Da almeno di quattromila anni, chi vive a contatto del Mare sa che le maree sono collegate alle fasi lunari. La relazione esatta, comunque, e' nascosta dietro molti fattori complicati, e alcune delle piu' grandi menti scientifiche degli ultimi quattro secoli hanno lavorato per comprndere, calcolare e predire la Marea. Galileo, Descartes, Kepler, Newton, Euler, Bernoulli, Kant, Laplace, Airy, Lord Kelvin, Jeffreys, Munk e molti altri hanno contribuito. Alcuni dei primi computer furono sviluppati per calcolare e prdirre la Marea. Ferrel costrui' una macchina che prevedeva la marea nel 1880 che e' stata usata dalla U. S. Coast and Geodetic Survey per predirre 19 costituenti della marea. Nel 1901, Harris estese la capacita' a 37 constituenti.

A dispetto di tutto questo lavoro rimangono domande importanti: Qual'e' l'ampiezza e la fase delle maree in ogni parte dell'oceano e lungo le coste? Qual'e' la velocita' e la direzione delle correnti di Marea? Qual'e' la forma delle maree nell'Oceano? Dove e' dissapata l'energia delle maree? Trovare le risposte a queste domande e' difficile, e le prime mappe globali, accurate delle maree di mare aperto sono state pubblicate solo nel 1994 (LeProvost et al., 1994). Il problema e' difficile perche' le maree sono un auto-gravitante, quasi-risonante, gorgogliare di acqua in un bacino oceanico rotatnte, elastico con dorsali, montagne e bacini sottomarini.

Predirre le maree lungo le coste e nei porti e' molto piu' semplice. I dati da un mareografo piu' la teoria delle forze di marea da' una accurata descrizione delle maree intorno al punto di misura.

Potenziale di Marea
Le maree sono calcolate dalle equazioni idrodinamiche per un oceano auto-gravitante su una Terra elastica rotante. La forza in gioco e' il piccolo cambiamento della gravita' dovuto al movimento della Luna e del Sole relativo alla Terra. Le piccole variazioni nella gravita' sorgono da due separati meccanismi. Per vedere come funzionano, consideriamo la rotazione della Luna intorno alla Terra.

1. La Luna e la Terra ruotano intorno al centro di massa del sistema Terra-Luna. Questo fa' nascere una accelerazione centripeta sulla superfice Terrestre che spinge l'acqua lontana dal centro di massa verso il lato della Terra opposto a quello della Luna.
2. Allo stesso tempo, la mutua attrazione gravitazionale della massa sulla Terra e sulla Luna causano all'acqua di essere attratta verso la Luna.

Se la Terra fosse un pianeta di solo oceano senza terraferma, e se l'oceano fosse molto profondo, i due processi dovrebbero produrre una coppia di rigonfiamenti di acqua sulla Terra, uno sul lato che guarda la Luna, uno sul lato opposto. Una chiara derivazione delle forze e' data da by Pugh (1987) e da Dietrich, Kalle, Krauss, e Siedler (1980). Qui vediamo la discussione in Pugh §3.2.

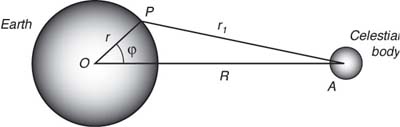Figura 17.10 Schema delle coordinate per determinare il potenziale che genera le maree.

Per calcolare l'ampiezza e la fase della marea di un pianeta oceanico, cominciamo dal calcolare le forze. Il potential di generazione della marea sulla superfice terrestre e' dovuto al sistema Terra-Luna che ruota intorno al centro comune di massa. Ignoriamo per ora la rotazione rerrestre su se stessa, La rotazione della Luna intorno alla Terra produce un potenziale V_M ad ogni punto sulla superfice della Terra

(17.5)

dove la geometria e' schematizzata nella Figura 17.10, g e' la costante gravitazionale, e M e' la massa della Luna. Dal triangolo OPA nella figura,

(17.6)

Usando questo nella (17.5) da'

(17.7)

r/R » 1/60, e (17.7) puo' essere espansa in potenze di r/R usando i polinomi di Legendre (Whittaker e Watson, 1963: §15.1):

(17.8)

Le forze mareali sono calcolate dal gradiente del potentiale, cosi' il primo termine nella (17.8) non produce forza. Il secondo termine produce una forza constante parallela ad OA. Questa forza mantiene la Terra in orbita intorno al centro di massa del sistema Terra-Luna. Il terzo termine produce le maree, assumendo che i termini piu' alti possono essere ignorati. Il potentiale che genera le maree e' quindi:

(17.9)

La forza generante la Marea puo' essere decomposta in componente perpendicolare P e parallela H alla superfice marina. La forza verticale produce cambiamenti molto piccoli nel peso degli oceani. Essa e' molto piccola compareta alla gravita', e puo' essere ignorata. La componente orizzontale e' mostrata in Figura 17.11. Essa e':

(17.10)

dove

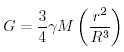(17.11)

Il potenziale di Marea e' simmetrico rispetto alla linea Terra-Luna, e produce rigonfiamenti simmetrici.

Figura 17.11 Componenti orizzontali delle forza di Marea sulla Terra quando il corpo che genera la marea e' sopra l'Equatore al punto Z(le frecce indicano solo la direzione, non l'intensita'). Da Dietrich, et al. (1980).

Se facciamo ruotare la nostra Terra coperta di oceano, un osservatore nello spazio vede i due rigonfiamenti fissi relativi alla linea Terra-Luna, mentre la Terra ruota. Ad un osservatore sulla Terra, i due rigonfiamenti di marea sembrano ruotare intorno alla Terra perche' la Luna si muove intorno al cielo a circa un giro al giorno. La Luna produce alte maree ogni 12 ore e 25.23 minuti all'equatore se la luna e' sopra l'equatore. Notare che le alte maree non sono esattamente due al giorno perche' la Luna sta anche ruotando ruotando intorno alla Terra. Naturalmente, La Luna e' sopra l'equatore soltanto due volte ogni mese lunare, e questo complica il nostro semplice schema delle maree in una ideale Terra coperta dall'Oceano. Inoltre, la distanza della Luna dalla Terra R varia perche' l'orbita lunare e' ellittica elliptical e perche' l'orbita ellittica non e' fissa.

Chiaramente, il calcolo delle maree sta diventando piu' complicato di quanto potevamo pensare. Prima di continuare, notiamo che le forze mareali del Sole sono derivate in maniera analoga. L'importanza relativa del sole e della Luna sono quasi le stesse. Sebbene il Sole sia molto piu' grande della Luna, e' molto piu' lontano.

	(17.12)
	(17.13)
	(17.14)

dove R_sun e' la distanza dal Sole, e S e' la massa del Sole, R_moon e' la distanza dalla Luna, e M e' la massa della Luna.

Coordinate dal Sole e della Luna
Prima di procedere oltre, abbiamo bisogno di conoscere la posizione della Luna e del Sole relativi alla Terra. Una accurata descrizione delle posizioni in tre dimensioni e' molto difficile, ed involve la conoscenza di termini arcani e di concetti di meccanica celeste. Qui, presento una descrizione molto semplificata da Pugh. Vedi anche Figura 4.1.

Un naturale sistema di riferimento per un osservatore dalla Terra e' il sistema equatoriale descritto all'inizio del Capitolo 3. In questo sistema, le declinazioni δ di un corpo celeste sono misurate a nord e a sud di un piano che taglia l'equatore della Terra.

Le distanze angolari intorno al piano sono misurate relativamente al punto sull'equatore celeste che e' fisso rispetto alle stelle. Il punto scelto per questo sistema e' l' equinozio invernale, chiamato anche il 'Primo punto dell'Ariete'... L'angolo misurato verso est, tra l'Ariete e l'intersezione equatoriale del meridiano tra un oggetto celeste e' chiamato right ascension dell'oggetto. La declinazione e la right ascension insieme definiscono la posizione dell'oggetto sulla volta celeste...

[Un altro sistema naturale di riferimento] usa il piano di rivoluzione della Terra intorno al Sole come riferimento. L'estenzione celeste di questo piano, che e' tracciato dall'annuale movimento apparente del Sole, e' chiamato l'eclittica. Convenientemente, il punto su questo piano che e' scelto come riferimento di zero e' ancora l'equinozio vernale, quando il Sole attraversa il piano equatoriale da sud a nord intorno il 21 Marzo di ogni anno. Gli oggetti celesti sono localizzati dalla loro latitudine e longitudine eclittica. L'angolo tra i due piani e' ,di 23.45°, e' chiamato obliquita' dell'eclittica... Pugh (1987: 72).

Frequenze di Marea
Ora, possiamo far ruotare la Terra intorno al suo asse polare. Il potential che puo' cambiare ad un punto geografico fissato sulla Terra e':

(17.15)

dove φ_p e' la latitudine a cui il potenziale di marea e' calcolato, δ e la declinazione della Luna o del Sole a nord dell'equator, e τ₁ e' l'angolo orario della Luna o del Sole. L'angolo orario e' la longitudine dove il piano immaginario del Sole o della Luna e l'asse di rotazione terrestre attraversano l'Equatore.

Il periodo dell'angolo orario solare e' il giorno solare di 24 ore 0 minuti. Il periodo dell'angolo orario lunare e' il giorno lunare di 24 ore 50.47minuti.

L'asse di rotazione della Terra e' inclinato di 23.45° rispetto al piano dell'orbita terrestre intorno al Sole. Questo definisce l'eclittica, e le declinazioni del Sole variano tra d = ± 23.45° con un periodo di un anno solare. L'orientazione dell'asse di rotazione terrestre precede rispetto alle stelle con un periodo di circa 26 000 anni. La rotazione del piano dell'eclittica produce a d ed all'equinozio vernale di cambiare lentamente, ed il movimento e' detto precessione degli equinozi.

L'orbita della Terra intorno al Sole e' ellittica, con il Sole in un fuoco. Il punto dell'orbita dove la distanza tra il Sole e la Terra e' al minimo e' detta perigeo. L'orientazione dell'ellisse nel piano dell'eclittica cambia lentamente nel tempo, causando al perigeo di ruotare con un periodo di 20 900 anni. Quindi R_sun varia con questo periodo.

Anche l'orbita della Luna e' ellittica, ma una descrizione dell'orbita lunare e' molto piu' complicata della descrizione dell'orbita solare. Di seguito ci sono alcuni punti base. L'orbita lunare giace su un piano inclinato con un angolo medio di 5.15° relativo al piano dell'eclittica. La declinazione lunare varia tra d = 23.45 ± 5.15° con un periodo di mese tropicale di 27.32 giorni solari. L'attuale inclinazione dell'orbita lunare varia tra 4.97°, e 5.32°.

La forma dell'orbita lunare varia pure. Primo, il perigeo ruota con un periodo di 8.85 anni. L'eccentricita' dell'orbita ha un valore medio di 0.0549, e varia tra 0.044 e 0.067. Secondo, il piano dell'orbita lunare ruota intorno alla'asse terrestre con un periodo di 17.613 annis. Entrambi i processi causano variazioni nel raggio R_moon.

Notare che sono un po' impreciso nel definire la posizione del Sole e della Luna. Lang (1980: §5.1.2) da' delle definizioni molto piu' precise.

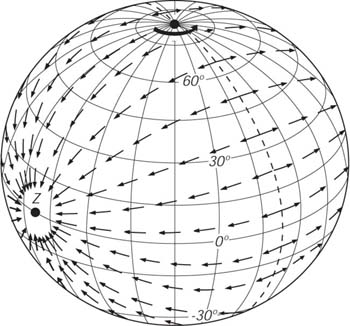
Sostituendo la (17.15) nella (17.9) abbiamo:

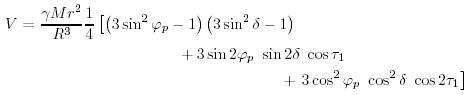(17.16)

L'equazione (17.16) separa il periodo del potenziale mareale lunare in tre termini con periodi intorno a 14 giorni, 24 ore, e 12 ore. Similarmente il potenziale solare ha periodi intorno a 180 giorni, 24 ore, e 12 ore. In questo modo ci sono tre distinti gruppi di frequenze di marea: semidiurne, diurne, ed a lungo periodo, aventi differenti fattori latitudinali sin² q, sin 2q, e (1 - 3 cos² q ) / 2, dove e' la co-latitude ( 90° - j ).

Doodson (1922) espanse la (17.16) in una serie di Fourier usando le frequenze giustamente scelte della Tabella 17.1. Altre scelte delle frequenze fondamentali sono possibili, per esempio il tempo solare locale medio puo' essere usato invece del tempo lunare locale medio. L'espansione di Doodson, comunque, porta ad una elegante decomposizione dei costituenti di marea in gruppi con frequenze e variabilita' spaziale simili.

Usando l'espansione di Doodson, ogni constituente della Marea ha una frequenza

(17.17)

dove gli interi n_i sono i numeri di Doodson. n₁ = 1, 2, 3 e n₂ - n₆ sono tra -5 and + 5. Per evitare i numeri negativi, Doodson aggiunse cinque a n_{2 · · · 6}. Ogni costituente di marea, talvolta chiamato marea parziale, ha un numero di Doodson. Per esempio, la principale marea lunare semi-diurna ha il numero 255.555. Poiche' la modulazione a molto lungo termine dovuta al cambiamento del perigeo del Sole e' molto piccola, l'ultimo numero di Doodson n₆ e' generalmente ignorato.

Se il potenziale di marea e' espanso in serie di Fourier con le frequenze di Doodson, e se la superfice oceanica e' in equilibrio con il potenziale di marea, il piu' grande costituente di marea dovrebbe avere frequenze e ampiezze date dalla tabella 17.2. La espanzione mostra che le maree con frequenze vicine ad uno o due cicli per giorno sono divise in linee molto vicine tra loro con spazi di separazione di un ciclo per mese. Ognuna di queste linee e' ulteriormente divisa in linee con spazi di separazione di un ciclo per anno (Figura 17.12). Inoltre, ognuna di queste linee e' divisa in linee con spazi di un ciclo per 8.8 anni, e cosi' via. Chiaramente, ci sono molti possibili costituenti di marea.

Perche' le linee di marea nella Figura 17.12 sono divise in cosi' tanti costituenti? Per rispondere alla domanda, supponiamo che l'orbita ellittica della Luna sia nel piano equatoriale della Terra δ = 0. Dalla (17.16), il potenziale di marea all'equatore, dove φ_p = 0, e':

(17.18)

Se l'ellitticita' dell'orbita e' piccola, R = R₀ ( 1 + ε ) , e la (17.18) e' approssimativamente

(17.19)

dove α = ( γ Mr ² ) / ( 4 R³ ) e' una constante. ε varia con un periodo di 27.32 giorni, e possiamo scrivere e = b cos( 2 π f₂) dove b e' una piccola costante. Con queste semplificazioni, la (17.19) puo' essere scritta:

	(17.20a)
	(17.20b)

che ha uno spettro con tre linee a 2 f₁ e 2 f₁ ± f₂. Quindi, la lenta modulazione dell'ampiezza del potenziale di marea a due cicli per giorno lunare costringe a dividere il potenziale di marea in tre frequenze. Questo e' il modo in cui le radio AM a modulazione di ampiezza lavorano. Se noi aggiungiamo un lento cambiamento alla forma dell'orbita, otterremo piu' termini anche in questo caso molto semplificato di una Luna in un orbita equatoriale.

Se siete degli osservatori molto attenti, avrete notato che lo spettro delle onde di marea nella Figura 17.12 non assomiglia allo spettro delle onde dell'Oceano della Figura 16.6. Le onde oceaniche hanno tutte le possibili frequenze, ed il loro spettro e' continuo. Le maree hanno frequenze precise determinate dalle orbite del Sole e della Luna, ed il loro spettro non e' continuo. Consiste di linee discrete.

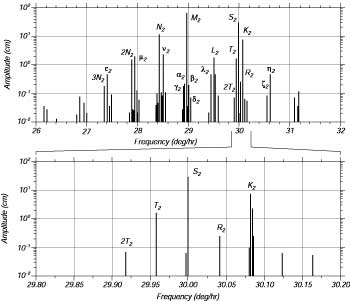Figura 17.12 In Alto: Spettro di maree con frequenze vicine alle semidiurne. Lo spettro e' diviso in gruppi separati da un ciclo per mese (0.55°/ora). In Basso: Spettro Espanso del gruppo S 2 , che mostra la divisione ad un ciclo per anno (0.04°/ora). La divisione piu' piccola in questa figura e' ad un ciclo 8.847 anni (0.0046°/ora).

Le espansioni di Doodson includono 399 costituenti, di cui 100 sono a lungo periodo, 160 sono diurni, 115 sono semi-diurni, e 14 sono tri-diurni. Molti hanno ampiezze molto piccole, e soltanto i piu' grandi sono inclusi nella tabella 17.2. I costituenti piu' importanti furono nominati da Sir George Darwin (1911) ed i nomi sono inclusi nella tabella. Cosi', per esempio, la principale marea semidiurna lunare, che ha il numero di Doodson 255.555, e' la M₂ , chiamata marea M-due.

17.5 Previsione della Marea

Se le maree nell'Oceano fossero in equilibrio con il potenziale di marea, la previsione dovrebbe essere molto piu' facile. Sfortunatamente, le maree sono lontane dall'equilibrio. Le onde in acqua poco profonda, come sono le maree, non si possono muovere abbastanza rapidamente da stare al passo con il Sole e la Luna. All'equatore, la marea avrebbe bisogno di propagarsi intorno al mondo in un giorno. Questo richiede una velocita' dell'onda intorno ai 460 m/s, che e' possibile solo in un Oceano profondo 22 km. In piu', i continenti interrompono la propagazione dell'onda. Come procedere?

Possiamo separare il problema della previsione della marea in due parti. La prima con la previsione delle maree nei porti ed in acque poco profonde dove le maree possono essere misurate con i mareografi. La seconda con la previsione delle maree negli oceani profondi dove le maree non possono essere misurate facilmente.

Previsione della Marea per Porti ed Acque Basse
Due metodi sono usati per predirre le maree future ad una stazione mareografica usando le passate misure del livello marino.

Il Metodo Armonico Questo e' il metodo tradizionale, e ancora ampiamente in uso. Il metodo usa decenni di osservazioni da un mareografo costiero dal quale l'ampiezza e la fase di ogni costituente (le armoniche di marea) sono calcolate dai dati misurati. Le frequenze usate nelle analisi sono specificate in anticipo dalle frequenze di base date nella Tabella 17.1.

A dispetto della sua semplicita', la technica ha alcuni svantaggi comparati con il metodo della risposta descritto piu' avanti.

1. Sono necessari piu' di 18.6 anni di dati per risolvere la modulazione delle fasi lunari.
2. Accuratezza dell'ampiezza di 10^-3 dei termini piu' grandi richiede che al minimo 39 frequenze devono essere determinate. Doodson trovo' che erano necessarie 400 frequenze per una accuratezza dell'ampiezza di 10^-4 per i termini piu' grandi.
3. La variabilita' non dovuta alla marea introduce grandi errori nelle ampiezze e nelle fasi calcolate dei costituenti di marea piu' piccoli. Le maree deboli hanno ampiezze piu' piccole della variabilita' alle stesse frequenze dovute ad altri processi come l'accumulo dovuto al vento ed alle correnti vicino al mareografo.
4. In molti porti, la marea e' non-lineare, e molte piu' costituenti di marea diventano importanti. Per alcuni porti, il numero di frequenze e' non maneggiabile. Quando le maree si propagano in un bacino molto poco profondo, specialmente gli estuari dei fiumi, l'onda si inclina e diventa non-lineare. Questo genera armoniche delle frequenze originali. In casi estremi, l'onda che avanza si inclina a tal punto di essere quasi verticale e si propaga come un muro d'acqua. Questo e' detto un mascaretto (tidal bore).

Il Metodo della Risposta Questo metodo, sviluppato da Munk e Cartwright (1966), calcola le relazioni tra le maree osservate in alcuni punti ed il potenziale di marea. La relazione e' la 'admittance' spettrale tra i maggiori costituenti di marea ed il potenziale di marea ad ogni stazione. La 'admittance' e' assunta essere una funzione di frequenza che varia lentamente in modo tale che la admittance dei maggiori costituenti puo' essere usata per determinare le risposte delle frequenze vicine. Le maree future sono calcolate moltiplicando il potenziale di marea per la funzione di admittance.

1. La tecnica richiede solo pochi mesi di dati.
2. Il potenziale di marea e' facilmente calcolato, e una conoscenza delle frequenze di marea non e' necessaria.
3. L'admittance e' Z(f) = G(f)/H(f). G(f) e H(f) sono le trasformate di Fourier del potenziale e dei dati del mareografo, e f e' la frequenza.
4. La admittance e' inversamente trasformata per ottenere l'admittance come funzione del tempo.
5. La tecnica funziona soltanto se le onde si propagano come onde lineari.

Previsione della Marea per Acque Profonde
La predizione delle maree in un oceano profondo e' molto piu' difficile di quella in acque basse perche' raramente i mareografi sono posizionati in acque profonde. Tutto cio' e' cambiato con il lancio del Topex/Poseidon. Il satellite fu posto in un orbita progettata espressamente per osservare le maree dell'Oceano (Parke et al., 1987) , ed il sistema altimetrico era sufficientemente accurato per misurare molti costituenti della marea. I dati del satellite sono stati usati per determinare le maree nell'oceano con una accuratezza di ± 2cm. Per molti scopi pratici, le maree sono ora accuratamente conosciute per la maggior parte dell'Oceano.

Molti approcci hanno portato a nuove conoscenze delle maree nell'oceano usando l'altimetria.

La Predizione Usando la Teoria Idrodinamica I calcoli puramente teorici delle maree non sono molto accurati, specialmente perche' la dissipazione dell'energia di mare non e' ben conosciuta. Tuttavia, i calcoli teorici forniscono indicazioni dei processi che influenzano le maree nell'oceano. Molti processi devono essere considereti:

1. Le maree in un bacino oceanico perturbano il campo gravitazionale terrestre, e la massa della protuberanza di marea attrae l'acqua dagli altri bacini oceanici. L'attrazione auto-gravitazionale delle maree deve essere considerata.
2. L'altezza del livello del mare nelle protuberanze mareali e' sufficientemente forte da deformare il fondo. La crosta si deforma come un solido elastico, e la deformazione si estende per migliaia di kilometri.
3. I bacini oceanici hanno una risonanza naturale vicina alle frequenze di marea. Il rigonfiamento di marea e' come un'onda in acqua bassa ruotante in un'oceano, e si propaga come un'alta marea che ruota lungo il bordo del bacino. Cosi' le maree sono un gorgogliare di acqua quasi risonante in un bacino oceanico. Le altezze della marea possono essere piu' alte dei valori di equilibrio della Tabella 17.2.
4. Le maree sono dissipate dall'attrito sul fondo in special modo in mari poco profondi, dal flusso intorno ai monti sottomarini ed alle dorsali midio-oceaniche, e dalla generazione di onde interne sopra queste strutture sommerse ed al bordo delle piattaforme continentali. Se la forzante di marea fosse fermata, le maree dovrebbero continuare ad agitare i bacini oceanici per molti giorni.
5. Poiche' la marea e' dovunque sulla Terra come un'onda in acqua poco profonda, la sua velocita' dipende dalla profondita'. Le maree si propagano piu' lentamente sulle dorsali medio-oceaniche e nei mari bassi. Quindi, la distanza tra i punti dei grigliati dei modelli numerici deve essere proporzionale alla profondita' con spaziature molto fitte nelle piattaforme continentali (LeProvost et al., 1994).
6. Le onde interne generate dalle maree producono un piccolo segnale sulla superfice marina vicino alle frequenze di marea, ma non sono in fase con il potential. Il rumore vicino alle frequenze delle maree produce dei picchi nello spettro delle elevazioni della superfice marina visti da Munk e Cartwright (1966). Il rumore e' dovuto alle onde interne generate dalle maree nel mare profondo.

Il Metodo della Risposta Piu' l'Altimetria Molti anni di dati altimetrici del Topex/Poseidon sono stati usati con il metodo della risposta per calcolare le maree di alto mare quasi ovunque dall'equatore al 66° (Ma et al., 1994). L'altimetro misura le altezze della superfice marina in coordinate geocentriche ad ogni punto lungo la traccia del satellite ogni 9.97 giorni. Il campionamento temporale sposta le frequenze delle maree verso le frequenze piu' grandi, ma i periodi spostati sono conosciuti molto bene e le maree vere possono essere ritrovate (Parke et al., 1987). Poiche' la registrazione della marea e' piu' corta di 8 anni, i dati dell'altimetro sono usati con il metodo della risposta per ottenere le predizioni per tempi molto piu' lunghi.

Recenti soluzioni da dieci differenti groppi, hanno una accuratezza ± 2.8cm nelle acque profonde(Andersen, Woodworth, e Flather, 1995). Il lavoro ha iniziato ad aumentare la conoscenza delle maree in acqua bassa.

Le mappe prodotte da questo metodo mostrano le caratteristiche piu' importanti delle maree di oceano profondo (Figure 17.13). La marea consiste in una cresta che ruota in senso anti-orario intorno ai bacini oceanici nell'emifhero nord ed in senso opposto nell'emisfero sud. I punti del minimo di marea sono detti amfidromici. Le maree piu' alte tendono a stare lungo la costa.

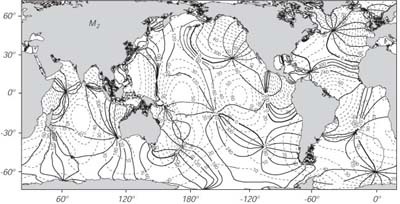Figura 17.13 Mappa globale della marea M2 calcolata dalle osservazioni del Topex/Poseidon delle altezze della superfice marina combinata con il metodo della risposta per estrarre le informazioni di marea. Le linee piene sono quelle con fase di marea costante, l' intervallo tra le linee e' di 30°. Le linee tratteggiate sono quelle di ampiezza constante, l'intervallo tra le linee e' di 10cm. Da Richard Ray, NASA Goddard Space Flight Center.

Altimetria Piu' Modelli Numerici I dati altimetrici possono essere usati direttamente con modelli numerici delle maree per calcolare le maree in tutte le aree dell'Oceano, dalle acque profonde a tutti i punti delle coste. Cosi' la tecnica e' particolarmente utile per determinare le maree vicino le coste e sopra le caratteristiche del fondo marino dove la traccia del satellite e' troppo distante per calcolare bene le maree dallo spazio. I modelli di marea usano griglie a elementi finiti simili a quello mostrato nella Figura 15.4. Recenti calcoli numerici di (LeProvost et al., 1994; LeProvost, Bennett, and Cartwright, 1995) danno maree globali con una accuratezza di ± 2-3 cm e risoluzione spaziale completa.

Ulteriori miglioramenti porteranno al limite dell'attuale precisione pratica, che e' di circa ±1-2 cm. Il limite e' posto dalle onde interne con frequenza di marea, e piccole variazioni a lungo termine della profondita' dell'oceano. Il cambiamento del contenuto di calore dell'oceano produce cambiamenti nella topografia oceanica di pochi centimetri, e questo cambia solo leggermente la velocita' delle onde in acque poco profonde.

La dissipazione di Marea
Le maree dissipano 3.75 ± 0.08 TW di potenza (Kantha, 1998), di cui 3.5TW sono dissipati nell'oceano, ed una quantita' molto piu' piccola nell'atmosfera e nella terraferma. La dissipazione aumenta la lunghezza del giorno di 2.07 millisecondi al secolo, questo aumenta il semiasse maggiore dell'orbita lunare di 3.86 cm/anno, e mescola le masse d'acqua dell'oceano.

I calcoli della dissipazione mareale dalle osservazioni del Topex/Poseidon sono notevolmente vicine alle stime della misura laser della distanza lunare, alle osservazioni astronomiche ed alle registrazioni delle antiche eclissi. La nostra conoscenza delle maree e' ora sufficientemente buona che possiamo cominciare ad usare le informazioni per studiare il mescolamento nell'Oceano. Ricorda, il mescolamento forza la circolazione abissale dell'Oceano come discusso nel §13.2 (Munk and Wunsch, 1998).

Chi avrebbe pensato che una comprensione dell'influenza dell'oceano sul clima dovrebbe richiedere una accurata conoscenza delle Maree?

17.6 Concetti Importanti

1. Le onde che si propagano in acque poco profonde sono rifratte dalle caratteristiche del fondo marino, ed eventualmente si rompono sulla spiaggia. La rottura delle onde guida le correnti vicino e lungo le spiagge, le correnti di ritorno, e le onde di taglio.
   
   
2. Le acque alte (Storm surges) sono forzate da venti forti durante le tempeste vicino alle spiagge. L'ampiezza di salita e' una funzione della velocita' del vento, la pendenza del fondo marino e la propagazione della tempesta.
   
   
3. Le Maree sono importanti per la navigaztione; influenzano le misure geodetiche accurate; e cambiano le orbite e la rotazione dei pianeti, le lune, e le stelle nelle galassie.
   
   
4. Le maree sono prodotte da una combinazione di potenziale gravitazionale della Luna e del Sole variabile nel tempo e delle forze centrifughe generate come se la Terra ruotasse nel comune centro di massa del sistema Terra-Luna.
   
   
5. Le maree hanno sei frquenze fondamentali. La marea e' la sovrapposizione di centinaia di costituenti di marea, ognuna avente una frequenza che e' la somma e la differenza delle cinque frequenze fondamentali.
   
   
6. Le maree in acque basse sono predette usando le misure della marea fatte in porti ed altre locazioni lungo la costa. Le registrazioni di Marea lunghe pochi mesi possono essere usate per predirre le maree per molti anni nel futuro.
   
   
7. Le maree nelle acque profonde sono calcolate da misure altimetriche, specialmente le misure Topex/Poseidon. In questo modo, le maree di acque profonde sono conosciute quasi ovunque con una accuratezza che si avvicina a ± 2 cm.
   
   
8. La dissipazione dell'energia di marea nell'Oceano trasferisce momento angulare dalla Luna alla Terra, provocando l'allungamento del giorno.
   
   
9. La dissipazione della marea mescola le masse di acqua, ed e' il maggior forzante della profonda meridional overturning circulation. Le maree, la circolazione abissale ed il clima sono legati fortemente.