Capitolo 6 - Temperatura,Salinita' e Densita'

I flussi di calore, l'evaporazione, la pioggia, lo sversamento dei fiumi, e lo scioglimento ed la formazione del ghiaccio marino, tutti influenzano la distribuzione della temperatura e della salinity alla superfice dell'oceano. I cambiamenti nella temperatura e nella salinita' possono aumentare o diminuire alla superfice la densita' dell'acqua, questo puo' portare alla convezione. Se l'acqua dalla superfice affonda dentro l'oceano piu' profondo, trattiene una relazione distintiva tra temperatura e salinita', che aiuta gli oceanografi a tracciare il movimento dell'acqua profonda. In aggiunta, La temperatura, la salinita' e la pressione sono usati per calcolare la densita'. La distribuzione della densita' dentro gli oceani e' direttamente connessa alla distribuzione dei gradienti orizzontali di pressione ed alle correnti dell'oceano. Per tutte queste ragioni, abbiamo bisogno di conoscere la distribuzione della temperatura, della salinita' e della densita' nell'oceano.

Prima di discutere della distribuzione della temperatura edella salinita', definiamo prima il significato dei termini, specialmente la salinita'.

6.1 Definizione della Salinita'

Al piu' semplice livello, la salinita' e' la quantita' totale in grammi di materiale dissolto in un kilogrammo di acqua marina. Percio' e' una quantita senza dimensioni. Non ha unita'. La variabilita' del sale disciolto e' molto bassa e bisogna stare molto attenti a definire la salinita' in modi che siano accurati e pratici. Per capire meglio il bisogno di accuratezza, guardiamo la Figura 6.1. Notiamo che la gamma della salinita' per molta acqua dell'oceano e' da 34.60 a 34.80 parti per migliaio, che e' 200 parti per milione. La variabilita' del Pacifico settentrionale profondo e' perfino piu' piccola, circa 20 parti per milione. Se vogliamo classificare l'acqua con differenti salinita', abbiamo bisogno di definizioni e strumenti per circa una parte per milione. Faccio notare che la gamma di temperatura e' molto piu' grande, circa 1°C, e che la temperatura e' piu' facile da misurare.

Scrivere una definizione pratica della salinita' e' difficile (vedi Lewis, 1980, per i dettagli), e varie definizioni sono state usate.

Figura 6.1 Iistogramma della temperatura e della salinita' dell'acqua fredda negli oceani. L'altezza e' proporzionale al volume. L'altezza del picco piu' alto corrisponde al volume di 26 milioni cubi di kilometri per una classe bivariata di 0.1° C e 0.01psu. Da Worthington (1981).

Una Semplice Definizione
In origine, la salinita' fu definita " la quantita' totale in grammi di materiale dissolto in un kilogrammo di acqua marina". Questa non e' utile perche il materiale dissolto e' quasi impossibile da misurare in pratica. Per esempio, come fai a misurare un materiale volatile come i gas? Nemmeno possiamo far evaporare l'acqua di mare per misurare il secco perche' i clori vanno persi nell'ultimo stadio dell'asciugamento. (Sverdrup, Johnson, e Fleming, 1942: 50).

Una Definizione piu' Completa
Per evitare queste difficolta', l'International Council for the Exploration of the Sea nel 1889, istitui' una commissione che raccomando' che la salinita' sia definita come "La quantita' totale dei materiali solidi in grammi dissolti in un kilogrammo di acqua marina, quando tutti i carbonati sono stati convertiti in ossidi, ed il bromo e lo iodio rimpiazzati dal cloro e tutta la materia organica completamente ossidata". La definizione fu pubblicata nel 1902. Questa e' utile ma difficile da usare tutti i giorni.

La Salinita' Basata sulla Clorinita'
Poiche' la definizione precedente era difficile da attuare nella pratica, ma poiche' la salinita' e' direttamente proporzionale alla quantita' di cloro nell'acqua di mare, e poiche' il cloro puo' essere misurato accuratamente da una semplice analisi chimica, la salinita' S fu ridefinita usando la clorinita':

dove clorinita' Cl e' definita come "la massa di argento richiesta per precipitare completamente gli alogeni in 0.328 523 4kg del campione di acqua marina."

Come le misure diventarono sempre piu' accurate, la (6.1) risulto' troppo inaccurata. Nel 1964 l'UNESCO ed altre organizzazioni internazionali designarono un Joint Panel sulle Oceanographic Tables and Standards per produrre una definizione piu' accurata. Il Joint Panel raccomando' nel 1966 (Wooster, Lee, e Dietrich, 1969) che la salinita' e la clorinita' siano messe in relazione usando:

Questo e' lo stesso come (6.1) per S = 35.

La Salinita' Basata sulla Conducibilita'
Allo stesso tempo che la (6.2) fu adottata, gli oceanografi avevano cominciato ad usare misuratori di conducibilita' per misurare la salinita'. Gli strumenti erano molto precisi e relativamente facili da usare comparati alle tecniche chimiche per misurare la clorinita'. Come risultato, il Joint Panel raccomando' anche che la salinita' era messa in relazione alla conducibilita' dell'acqua marina usando:

dove C (S, 15 , 0) e' la conducibilita' del campione di acqua marina a 15°C ed alla pressione atmosferica, avendo una salinita' S derivata dalla (6.4), e C (35 , 15 , 0) e' la conducibilita' dell'acqua di mare standard "Copenhagen". Millero (1996) out that (6.3) is not a new definition of salinity, it merely gives chlorinity as a function of conductivity of seawater relative to standard seawater.

Practical Salinity Scale of 1978
By the early 1970s, accurate conductivity meters could be deployed from ships to measure conductivity at depth. The need to reevaluate the salinity scale led the Joint Panel to recommend in 1978 that salinity be defined using only conductivity, breaking the link with chlorinity. All water samples with the same conductivity ratio have the same salinity.

The Practical Salinity Scale of 1978 is now the official definition:

where C (S, 15, 0) is the conductivity of the sea-water sample at a temperature of 15°C and standard atmospheric pressure, and C (KCl, t, 0) is the conductivity of the standard potassium chloride (KCl) solution at a temperature of 15°C and standard atmospheric pressure. The standard KCl solution contains a mass of 32.435 6 grams of KCl in a mass of 1.000 000kg of solution.

Lewis (1980) gives additional equations for calculating salinity at other temperatures:

An extension of (6.4) gives salinity at any pressure (see Millero 1996: 72).

Comments
The various definitions of salinity work well because the ratios of the various ions in sea water are nearly independent of salinity and location in the ocean (Table 6.1). Only very fresh waters, such as are found in estuaries, have significantly different ratios. The result is based on Dittmar's (1884) chemical analysis of 77 samples of sea water collected by the Challenger Expedition and further studies by Carritt and Carpenter (1958).

"The importance of this result cannot be over emphasized, as upon it depends the validity of the chlorinity: salinity: density relationships and, hence, the accuracy of all conclusions based on the distribution of density where the latter is determined by chemical or indirect physical methods such as electrical conductivity..." -Sverdrup, Johnson, Fleming (1942).

The relationship between conductivity and salinity has an accuracy of around ± 0.003 in salinity. The very small error is caused by variations in constituents such as SiO₂ which cause small changes in density but no change in conductivity.

Instruments for measuring salinity are calibrated using Normal Standard Seawater (P-series). The standard water is made from large samples of water from the north Atlantic, carefully diluted to S = 35, which is distributed in 275 ml sealed glass ampoules. Each is labeled for its conductivity ratio and salinity according to the Practical Salinity Scale 1978 and distributed worldwide by Ocean Scientific International in England since 1989. Each sample is carefully calibrated using the standard KCl solution.

6.2 Definizione di Temperatura

Molti processi fisici dipendono dalla temperatura; e pochi di questi processi possono essere usati per definire la temperatura assoluta T. L'unita' di misura di T e' il kelvin, che ha come simbolo K. I processi fondamentali usati per definire una scala di temperatura assoluta sulla gamma di temperature trovate in mare include (Soulen e Fogle, 1997): 1) la legge dei gas che collega la pressione alla temperatura di un gas ideale con le correzioni per la densita' del gas; e 2) il rumore del voltaggio di una resistenza R.

La misura di temperatura che usa una scala assoluta e' difficile e la misura e' di solito fatta dai laboratori nazionali per gli standard (in Italia: Istituto CNR Galileo Ferraris di Torino). Le misure assolute sono usate per definire una scala pratica di temperature assolute basata sulla temperatura di pochi punti fissi e congegni calibrati con quei punti fissi che interpolano la misura.

Per le temperature comunemente trovate in mare, il congegno interpolante e' il termometro al platino. Consiste in un filo di platino puro, non teso e - loosely wound- la cui resistenza e' una funzione altamente lineare della temperatura. Il sensore e' calibrato a punti fissi tra il punto triplo dell'idrogeno a 13.8033K , il punto di congelamento dell'argento 961.78 K, includendo il punto triplo dell'acqua a 0.060°C, il punto di fusione del Gallio a 29.7646°C, ed il punto di congelamento dell'Indio a 156.5985°C (Preston-Thomas, 1990). Il punto triplo dell'acqua e' la temperatura alla quale ghiaccio,acqua e wapore acqueo sono in equilibrio. La scala di temperatura in kelvin T e' collegata a quella di temperatura in gradi t [°C] da:

La scala pratica di temperatura e' stata rivista nel 1887, 1927, 1948, 1968, e nel 1990 quando cioe' venivano accettate determinazioni piu' accurate delle temperatura assoluta. La scala piu' recente e' l'International Temperature Scale del1990 (ITS-90). Differisce leggermente da quella del 1968 IPTS-68. A 0°C sono uguali, e sopra 0°C ITS-90 e' leggermente piu' fredda. t₉₀ - t₆₈ = -0.002 a 10°C, -0.005 a 20°C, 0.007 a 30°C e -0.010 a 40°C.

Da notare che mentre gli oceanografi usano termometri calibrati con una accuratezza di millesimo di grado, che e' 0.001°C, la scala della temperatura stessa ha errori piu' grandi: pochi millesimi di grado.

6.3 Distribuzione Geografica della Temperatura e Salinita' Superficiale

La distribuzione superficiale della temperatura tende ad essere zonale, cioe' tende ad essere indipendente dalla longitdine (Figura 6.2). Le acque piu' calde sono vicino all'equatore, le piu' fredde vicino ai poli. Le deviazioni da zonali sono poche. Al di sotto dei 40°, le acque piu' fredde tendono ad andare verso l'equatore nei lati orientali dei bacini. A Nord di quella latitudine, le acque piu' fredde tendono ad essere sul lato occidentale.

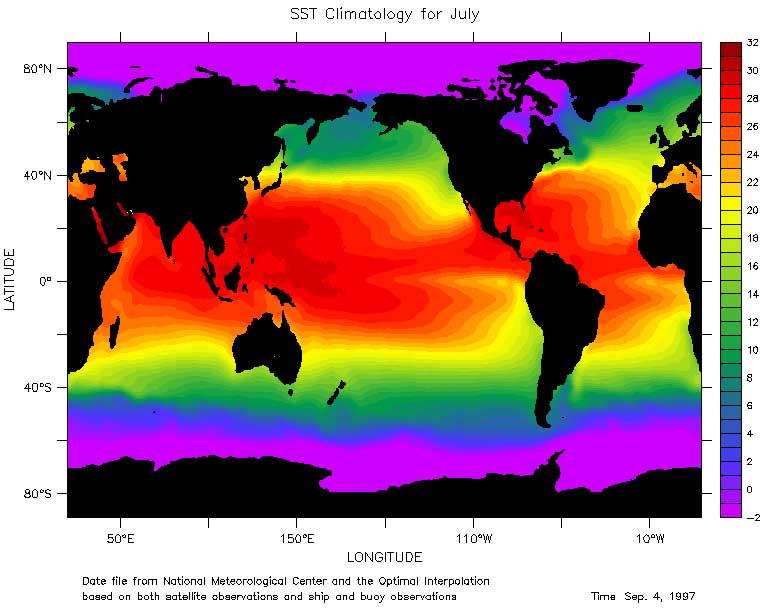
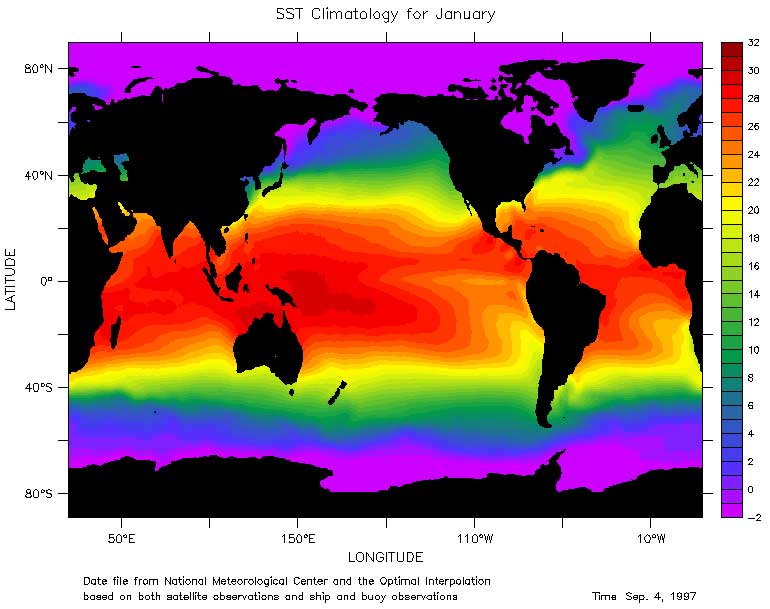
Figura 6.2 Temperature superficiali medie calcolate con la "tecnica di interpolazione ottimale" (optimal interpolation technique) (Reynolds and Smith, 1995) usando i rapporti delle navi e le misure di temperatura AVHRR.

Le anomalie della temperatura superficiale del mare, dalla media di lungo termine, sono piccole, inferiori a 1.5°C eccetto nel Pacifico equatoriale dove le deviazioni possono essere di 3°C (Figura 6.3: sopra).

L'intervallo di temperatura superficiale e' piu' grande alle medie latitudini, specialmente nella parte occidentale degli oceani. (Figura 6.3: sotto). Da occidente, l'aria fredda che soffia sopra i continenti in inverno, raffredda il mare. Il raffreddamento domina il bilancio del calore. Nei tropici l'intervallo di temperatura e' per lo piu' inferiore a 2°C.

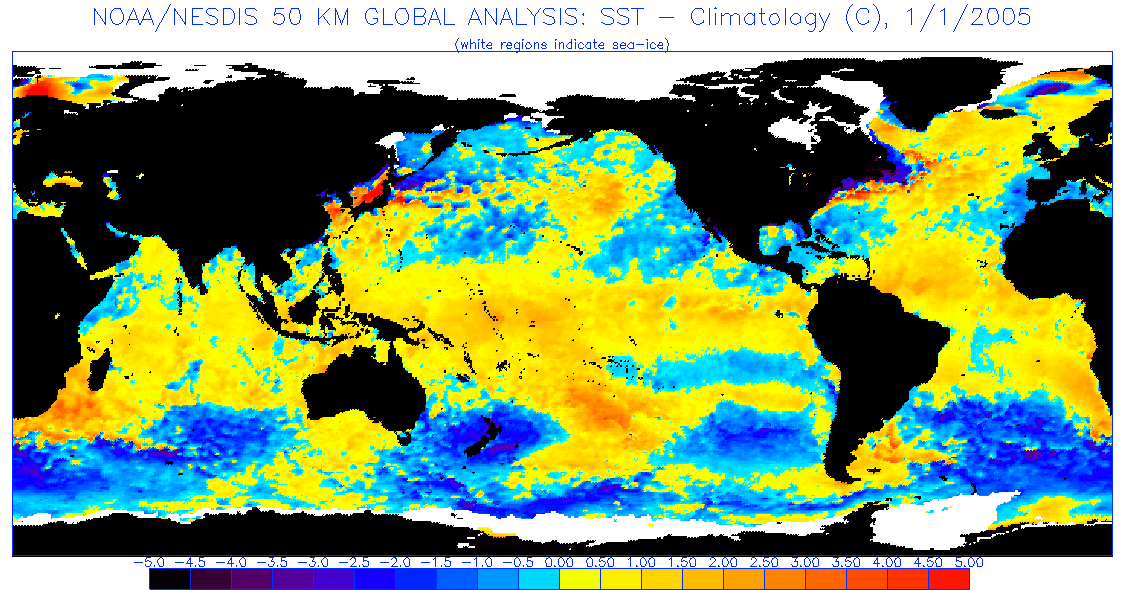
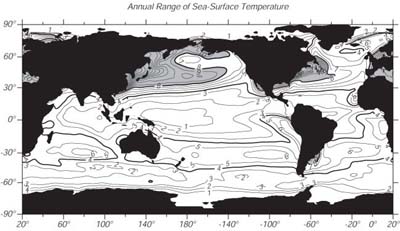
Figura 6.3
sopra: Le anomalie della temperatura superficiale del mare per Gennaio 2005 relative alla temperatura media mostrate in Figura 6.2 usando i dati pubblicati da Reynolds and Smith (1995) nel Climate Diagnostics Bulletin per il February 1995.

sotto: Intervallo annuale della temperatura superficialein °C calcolata da Reynolds and Smith (1995) Le isolinee sono ogni 1°C con linea in grassetto a 4°C ed a 8°C. Le aree ombreggiate eccedono gli 8°C.

Anche la distribuzione della salinita' superficiale tende ad essere zonale. Le acque piu' salate sono alle medie latitudini dove l'evaporazione e' alta. Le acque meno salate sono vicino l'equatore dove la pioggia apporta acqua dolce alle acque superficiali ed alle alte latitudini dove il mare ghiacciato che si sciolglie apporta acqua dolce. (Figure 6.4). La media zonale (east-west) della salinita'mostra una chiara correlazione tra salinita' ed evaporazione meno precipitazione e meno apporti fluviali (Figura 6.5).

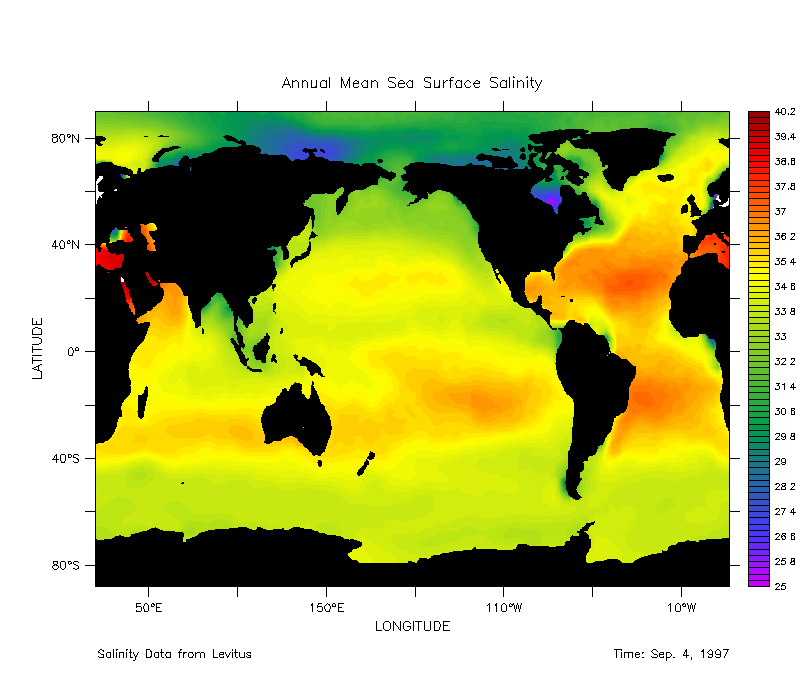Figura 6.4 Salinita' superficiale media. L'intervallo delle isolinee e' 0.25. Le aree ombreggiate eccedono 36. Da Levitus (1982).

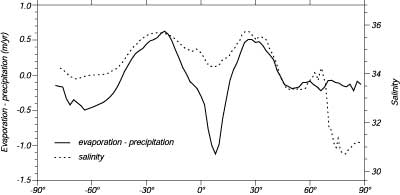Figura 6.5 Media Zonale della salinita' della superfice marina calcolata su tutti gli oceani da Levitus (1982) e la differenza tra evaporazione e precipitazione (E - P) calcolata dai dati mostrati in Figura 5.14.

Poiche' molti grandi fiumi confluiscono in Atlantico e nel Mare Artico, Perche' l'Atlantico e' piu' salato del Pacifico? Broecker (1997) ha mostrato che 0.32 Sv dell'acqua evaporata dall'Atlantico non cade come pioggia sulla terraferma. Invece, e' portata dai venti in Pacifico (Figure 6.6). Broecker sottolinea che la quantita' e' piccola, poco piu' grande del flusso del Rio delle Amazzoni, ma "questo flusso non fosse compensato da uno scambio di acqua Atlantica piu' salata con acqua Pacifica meno salata were this flux not compensated by an exchange of more salty Atlantic waters for less salty Pacific waters, La salinita' dell'intero Atlantico dovrebbe aumentare di un grammo di sale al litro per ogni millennio."

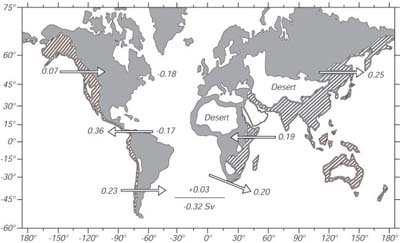Figura 6.6 Acqua trasportata dall'atmosfera dentro e fuori l'Atlantico. I bacini che drenano nell'Atlantico sono in grigio, i deserti in bianco, e gli altri bacini sono ombreggiati. Le frecce danno la direzione dei trasporti di acqua dell'atmosfera ed i valori sono in Sverdrup. I numeri in grassetto danno il trasporto netto per l'Atlantico. Complessivamente, l'Atlantico perde 0.32Sv, una quantita' uguale al flusso del Rio delle Amazoni. Da Broecker (1997).

Temperatura e Salinita' Media dell'Oceano La temperature media dell'acqua dell'oceano e': t = 3.5°C; e la salinita' media e' S = 34.7. La distribuzione sulla media e' piccola: 50% dell'acqua e' dentro l'intervallo:

6.4 Lo Strato Mescolato ed il Termoclino

Il vento che soffia sopra il mare mescola gli strati superiori e forma, alla superfice dell'oceano, un sottile strato mescolato (mixed layer) che ha temperature e salinita' costanti dalla superfice fino ad una profondita' dove i valori differiscono da quelli della superfice. La grandezza della differenza e' arbitraria, ma tipicamente la temperatura al fondo dello strato non deve essere piu' di 0.02-0.1°C piu' fredda di quella alla superfice. Da notare che entrambe temperatura e salinita' devono essere costanti nel "mixed layer". Vedremo piu' avanti che la velocita' media non e' costante. Lo strato mescolato e' profondo circa 10-200 m su molte zone dei tropici e delle medie latitudini.

Lo spessore e la temperatura del "mixed layer" variano da giorno a giorno e da stagione a stagione in risposta a due fattori:

1. I flussi di calore attraverso la superfice riscaldano e raffreddano le acque superficiali. I cambi in temperatura cambiano la differenza di densita' tra strato rimescolato e le acque sottostanti. Piu' grande e' la differenza, e piu' lavoro e' necessario per mischiare gli strati sottostanti e viceversa.
2. La turbolenza nel "mixed layer" mescola il calore verso il basso. La Turbolenza dipende dalla velocita' del vento e dalla intensita' delle onde che si rompono. La turbolenza mescola l'acqua dello strato e mescola l'acqua dello strato con quella del termoclino.

Il "mixed layer" alle medie latitudini e' piu' sottile nella tarda estate quando i venti sono piu' deboli, ed il sole riscalda gli strati superficiali (Figura 6.7). Alle volte, il calore e' cosi' forte ed i venti cosi' deboli, che lo strato e' di soli pochi metri. In Autunno, le prime tempeste mescola il calore verso il basso e lo spessore dello strato aumenta, ma un po' di calore e' perso. In Inverno, il calore e' perso, ed il "mixed layer" continua ad approfondire, raggiungendo il massimo nel tardo inverno. In Primavera, i venti si indeboliscono, la luce solare aumenta ed un nuovo "mixed layer" si forma.

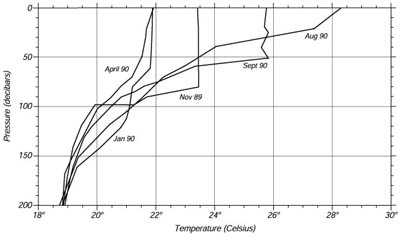Figura 6.7 Crescita e decadimento dello strato mescolato e del termoclino da Novembre 1989 a Settembre 1990 alla Bermuda Atlantic Time-series Station (BATS) 31.8°N 64.1°W. I dati sono stati raccolti dalla Bermuda Biological Station for Research, Inc. Da notare che i valori di pressione in decibar sono quasi uguali alle profondita' in metri (vedi §6.8 per la definizione di decibar).

Sotto lo strato mescolato, la temperatura dell'acqua diminuisce rapidamente con la profondita', eccetto che alle alte latitudini. L'intervallo di profondita' dove il tasso di cambiamento: il gradiente della temperatura e' grande, e' chiamato thermocline. Poiche' la densita' e' strettamente collegata alla temperatura, il termoclino tende ad essere lo strato dove il gradiente di densita' e' piu' grande, il pycnocline.

La cima del termoclino varia sensibilmente con le stagioni come si vede nell'intervallo tra 20 e 200 decibar della Figura 6.7. Questo e' il termoclino stagionale. Il termoclino permanente si estende da sotto il termoclino stagionale a profondita' di1500-2000m (Figura 6.8). Alle alte latitudini, come nella stazione alla AAC della figura, ci puo' essere uno strato piu' freddo e meno salato sopra il termoclino permanente.

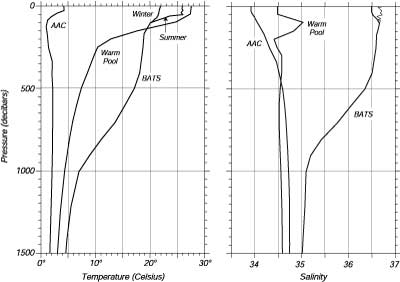Figura 6.8 Profili tipici di temperatura e salinita' in ocean aperto. AAC: A 62.0°S, 170.0°E nella Antarctic Circumpolar Current del16 Gennaio1969 misurata dalla R/V Hakuho Maru. "Warm Pool" (Sacca Calda): A 9.5°N, 176.3°E nel Pacifico tropicale occidentale il12 March 1989 misurato da Bryden e Hall dalla R/V Moana Wave. BATS: A 31.8°N, 64.1°W vicino Bermuda il 17 April ed il 10 September 1990 misurato dalla Bermuda Biological Station for Research, Inc. I dati sono inclusi nel Java Ocean Atlas.

Lo strato mescolato tende ad essere piu' salato che nel termoclino tra 10° e 40° di latitudine, dove l'evaporazione eccede la precipitazione. Ad alte latitudini il"mixed layer" e' meno salato perche' la pioggia ed il ghiaccio che si scioglie riduce la salinita'. In alcune regioni tropicali, come nel Pacifico tropicale occidentale, la pioggia produce un sottile "mixed layer" meno salato.

6.5 Densita', Temperature Potenziale e Densita' neutrale

Durante l'inverno, l'acqua fredda, che si forma alla superfice, sprofonda alla profondita' determinata dalla sua densita' relativa a quella dell'acqua piu' profonda. Le correnti trasportano l'acqua in altre parti dell'oceano. succede sempre che l'acqua si muove per stare sotto all'acqua meno densa e sopra a quella piu' densa. La distribuzione delle correnti dentro l'oceano dipende dalla distribuzione della pressione, che dipende dalle variazioni della densita' dentro l'oceano come vedremo nel §10.4. Cosi', se vogliamo seguire i movimenti dell'acqua dentro l'oceano, abbiamo bisogno di conoscere la distribuzione della densita' nell'oceano.

Densita' e sigma-t
I calcoli dei movimenti di acqua richiedono misure di densita' con una accuratezza di poche parti per milione. Questo non e' facile

La Densita' Assolutadell'acqua puo' essere misurata solo in laboratori speciali e con grande difficolta'. La migliore accuratezza e' 1: 2.5 × 10⁵ = 4 parti per milione.

Per evitare la difficolta' di lavorare con densita' assolute, gli oceanografi usano la densita' relativa alla densita' dell'acqua pura. La densita' ρ(S, t, p) e' ora definita usando gli Standard Mean Ocean Water di composizione isotopica conosciuta, assumendo la saturazione dei gas atmosferici dissolti. Dove S, t, p si riferiscono a salinita', temperatura, e pressione.

In pratica, la densita' non e' misurata, e' calcolata da misure in situ of pressione, temperatura, e conducibilita' usando l'equazione di stato dell'acqua di mare. Questo puo' essere fatto con una accuratezza di due parti per milione.

La densita' dell'acqua al livello del mare e' tipicamente 1027 kg/m³. Per semplificare, gli oceanografi spesso consideranosolo le ultime 2 cifre della densita', una quantita' che chiamano anomalia della densita' (density anomaly) or Sigma (s, t, p):

σ (S, t, p) e' tipicamente 27.00 kg/m³. Il Gruppo di Lavoro sui Simboli in Oceanografia raccomanda che deve essere rimpiazzato, perche' era originariamente definito relativo all'acqua pure ed era un valore adimensionale. Di seguito, comunque, seguire la pratica comune ed in uso σ.

Se stiamo studiando gli strati superficiali del mare, possiamo ignorare la compressibilita', ed usiamo una nuova quantita' sigma-t (scritta σ_t):

Questa e' l'anomalia della densita' di un campione di acqua quando la pressione totale su di lui e' stata ridotta alla sola pressione atmosferica (i.e. zero water pressure), ma la temperatura e la salinita' sono valori in situ .

Temperatura Potenziale
Consideriamo una porzione di acqua sotto lo strato mescolato, il contenuto di sale e di calore puo' cambiare soltanto con il mescolamento con altre acque. Allora possiamo usare misure di temperatura e salinita' per tracciare il cammino percorso dalla porzione di acqua in esame. Questo e' fatto meglio se rimuoviamo l'effetto della compressibilita'.

Come l'acqua affonda, la pressione aumenta, l'acqua e' compressa, e la compressione esercita un lavoro sull'acqua. Questo causa il riscaldamento dell'acqua. Per comprendere il riscaldamento, consideriamo un cubo contenente una quantita fissata di acqua. Come il cubo affonda, si comprime ed i suoi lati muovono all'interno. Ricordando che il lavoro e' la forza per lo spostamento, il lavoro e' lo spostamento dei lati del cubo per la forza esercitata dalla pressione. L'energia trasformata in calore e' piccola, ma rilevabile
The heating is small but noticeable compared with the small changes of the temperature of the adjacent water
(Figure 6.9).

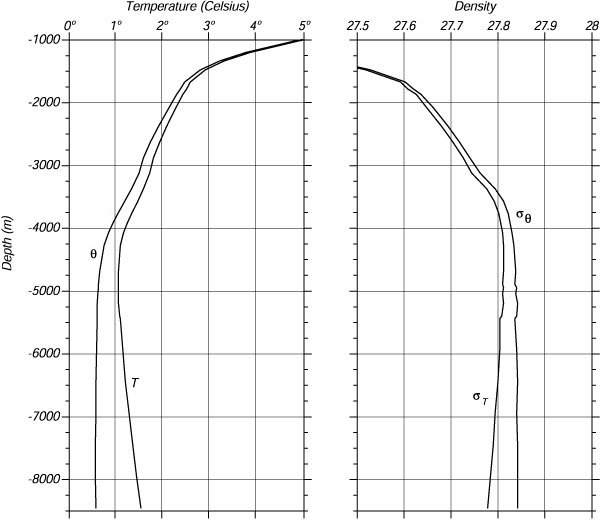Figura 6.9 Profili di temperatura Sinistra in situ e potenziale e Destra sigma-t e sigma-theta misurati da bordo della R/V Eltanin nella Fossa di Kermadec (Pacifico) durante la Scorpio Expedition del 13 Luglio1967 a 175.825°E and 28.258°S. Da Warren (1973).

Per rimuovere l'influenza della compressibilita' dalle misure di temperatura, gli oceanografi (ed i metereologi che hanno lo stesso problema in atmosfera) usano il concetto di temperatura potenziale. Temperatura Potenziale θ e' definita come la temperatura di una porzione di acqua al livello del mare dopo che e' stata sollevata adiabaticamente dalla profondita' a cui era nell'oceano. Sollevare la porzione adiabaticamente significa che non ha avuto scambi di calore con l'acqua circostante. Naturalmente non e' stata portata alla superfice. La temperatura potenziale e' calcolata dalla temperatura dell'acqua a quella profondita': la temperatura in situ, e dalla profondita'.

Densita' Potenziale
Se stiamo studiando gli strati intermedi dell'oceano, diciamo a profondita' vicine al kilometro, non possiamo ignorare la compressibilita'. Poiche' i cambiamenti in pressione influenzano principalmente la temperatura dell'acqua, l'influenza dell'acqua puo' essere rimossa, in prima approssimazione, usando la densita' potenziale.

Densita' potenziale σ_θ e'la densita' che ha una porzione di acqua se fosse sollevata adiabaticamente fino alla superfice senza cambiamenti anche di salinita'.

σ_θ e' specialmente utile perche' e' una propieta' termodinamica conservata.

La densita' potenziale non e' utile per comparare densita' dell'acqua a grandi profondita'. Se portiamo porzioni di acqua alla superfice e compariamo le loro densita', i calcoli della densita' potenziale ignorano gli effetti della pressione sui coefficienti dell'espansione termale e della salinita'. Come risultato, due campioni d'acqua aventi la stessa densita', ma differenti temperature e salinita' ad una profondita' di quattromila metri, possono avere notevoli differenze di densita' potenziale. In alcune regioni, l'uso della σ (θ) puo' portare ad un apparente diminuizione di densita' con la profondita' (Figura 6.10) sebbene sappiamo che cio' non e' possibile perche' una tale colonna d'acqua dovrebbe essere instabile.

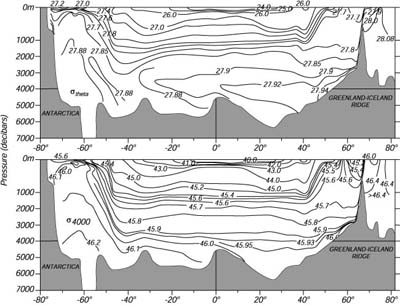Figura 6.10 Sezioni verticali della densita' nell'Atlantico occidentale. Notare che la scala della profondita' cambia a 1000m. Sopra: σθ, mostra un apparente inversione di densita' sotto i 3000m. Sotto: σ4 mostra un continuo aumento della densita' con la profondita'. Da Lynn e Reid (1968).

Per comparare campioni di grande profondita', e' meglio portare entrambi i campioni ad una profondita' vicina piuttosto che al livello del mare p = 0. Per esempio, possiamo portare tutti i campioni ad una pressione di 4000 decibar, che e' vicino ad una profondita' di 4km:

dove σ₄ e' la densita' di una porzione di acqua portata adiabaticamente a 4,000 decibar. Piu' generalmente, gli oceanografi talvolta usano σ_r

dove p e' la pressione, e p_r e' la pressione ad un qualche livello di riferimento. Nella (6.8) il livello e' p_r = 0 decibar, e in (6.9) p_r = 4000 decibar.

L'uso di σ_r porta a problemi. Se si vuole seguire la porzione di acqua profonda nell'oceano, possiamo usare la σ₃ in alcune aree, e la σ₄ in altre. Ma che cosa succede quando una porzione di acqua si muove da una profondita' di 3 km in un'area ad un altra alla profondita' di 4 km? C'e' una differenza tra la densita' di una porzione espressa dalla σ₃ comparata con la densita' espressa dalla σ₄. Per evitare questa difficolta, Jackett and McDougall (1997) proposero una nuova variabile che chiamarono densita' neutrale.

Surperfice e Densita' Neutrale
Una porzione di acqua si muove localmente lungo un percorso di densita' costante mantenendosi sotto acqua meno densa e sopra a quella piu' densa. Piu' precisamente, si muove lungo un percorso di densita' potenziale costante σ_r riferito alla profondita' locale r. Tale cammino e' chiamato cammino neutrale (neutral path) (Eden e Willobrand, 1999). Un elemento di superfice neutrale e' la superfice tangente al cammino neutrale attraverso un punto dell'acqua. Nessun lavoro e' richiesto per muovere una porzione su questa superfice, perche' non c'e' forza di galleggiamento che agisce sulla porzione e la muove (se ignoriamo la frizione).

Seguiamo ora la porzione come si muove lontano dalla regione locale. Questo puo' essere fatto con approssimazioni, ma non con esattezza. Per prima cosa, possiamo pensare che, poiche' conosciamo ovunque le tangenti alla superfice, possiamo definire una superfice che sia l'inviluppo delle tangenti. Ma una superfice esatta non e' matematicamente possibile nell'oceano reale, sebbene possiamo andarci molto vicino.

Jackett and McDougall (1997) svilupparono una variabilepratica ed una superfice pratica della densita' neutrale γ ⁿ che sta dentro pochi metri di una superfice ideale per ogni parte dell'oceano. Costruirono le loro variabili usando i dati degli atlanti di Levitus (1982). I valori della densita' neutrale furono usati per etichettare i dati negli atlanti di Levitus. Questo dataset di dati pre-etichettati e' usato per calcolare la γⁿ in nuove posizioni dove t, S sono misurate come una funzione della profondita' di interpolazione dei quattro punti piu' vicini degli atlanti di Levitus. Attraverso questa procedura, la densita' neutrale γⁿ e' una funzione della salinita' S, in situ della temperatura t, della pressione p, della longitudine e della latitudine.

La superfice neutrale definita sopra, differisce solo di poco da una superfice neutrale ideale. Se una porzione di acqua si muove intorno ad un "gyre" (vortice oceanico di 100-200 km di diametro) su una superfice neutrale e ritorna alla sua locazione di partenza, la sua profondita' differira' di circa 10m da quella di partenza. Se si usano le superfici di densita' potenziali, la differenza puo' essere di centinaia di metri: di gran lunga un errore piu' grande.

Equazione di stato dell'acqua di mare
La densita' dell'acqua di mare e' misurata raramente. La densita' e' calcolata da misure di temperatura, di conducibilita' o salinita', e di pressione usando l'equazione di stato dell'acqua marina. L'equazione di stato e' una equazione che relaziona la densita' alla temperatura, alla salinita', ed alla pressione.

L'equazione e' stata derivata dall'approssimare le curve della densita' misurata in laboratorio con una funzione della temperatura, della pressione, e della salinita', clorinita' o conducibilita'. La International Equation of State (1980) pubblicata dal Joint Panel on Oceanographic Tables and Standards (1981) e' attualmente usata. Vedianche Millero e Poisson (1981) e Millero et al., (1980). L'equazione ha una accuratezza di 10 parti per milione, che e' 0.01 unita di σ(θ).

Non ho scritto per esteso l'equazione di stato perche' consiste di tre polinomi con 41 contanti (JPOTS, 1991).

Accuratezza della Temperatura, della Salinita' e della Densita'
Se vogliamo distinguere le differenti masse di acqua dell'oceano e se la gamma delle temperature e delle salinita' e' piccola come quella della Figura 6.1, allora dobbiamo misurare la temperatura, la salinita' e la pressione con grande cura. Abbiamo bisogno di un errore di poche parti per milione.

Tali accuratezze possono essere raggiunte solo se tutte le quantita' sono definite attentamente, se tutte le misure sono fatte con grande cura, se tutti gli strumenti sono accuratamente calibrati e se tutte le procedure sono fatte in accordo agli standard accettati internazionalmente. Gli standard sono spiegati nel Processing of Oceanographic Station Data (JPOTS, 1991) pubblicato dall'UNESCO. Il libro contiene le definizioni delle variabili primarie accettate internazionalmente ed le procedure per misurare le variabili primarie. Descrive anche i metodi accettati per calcolare le quantita derivate dalle variabili primarie come la temperatura potenziale, la densita', la stabilita', ecc....

6.6 La Misura della Temperatura

La temperatura dell'oceano e' stata misurata in molti modi. I termometri al mercurio ed i termistori sono comunemente usati sulle navi e sulle boe. Sono calibrati in laboratorio prima di essere usati, e se possibile anche dopo, usando termometri al mercurio o al platino con una accuratezza tracciata da laboratori nazionali degli standard. Anche i radiometri all'infrarosso su satelliti misurano la temperatura superficiale del mare.

Termometri al Mercurio
Questo e' il termometro, non elettronico, piu' comunemente usato. E' usato molto spesso, in contenitori, calati da un bordo della nave per misurare la temperatura in superfice, oppure su bottiglie Nansen per misurare temperature in profondita' , si usano anche in laboratorio per calibrare altri termometri. Con calibrazioni molto precise l'accuratezza e' circa ± 0.001°C.

Un termometro al mercurio molto importante e' il termometro a rovesciamento (Figure 6.11) posizionato sulle bottiglie Nansen che sono descritte nella prossimaq sezione. E' un termometro che ha un restringimento nella colonnina di mercurio che causa alla vena del fluido di spezzarsi ad un punto ben preciso, quando il termometro e' capovolto. Il termometro e' calato nel mare in posizione normale; e di stabilizzarsi alla temperatura dall'acqua. Il mercurio si espande nella colonnina e la quantita' di mercurio nella colonna e' proporzionale alla temperatura. Il Termometro e' quindi capovolto, la vena di mercurio si interrompe, intrappolando il mercurio nella colonna, Il termometro ritorna con questa posizione in superfice. Il mercurio nella colonna del termometro a rovesciamento e' letto su ponte insieme alla temperatura di un termometro normale, che da' la temperatura alla quale il termometro a rovesciamento e' stato letto. Le due letture danno la temperatura dell'acqua alla profondita' dove il termometro e' stato capovolta.

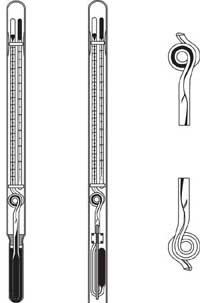Figura 6.11 Sinistra: Termometro a rovesciamento protetto e non protetto, in posizione prima del rovesciamento. Destra: La parte ristretta della colonna in posizione normale e rovesciata. Da von Arx (1962).

Il termometro a rovesciamento e' inserito in un tubo di vetro, che lo protegge dalla pressione, poiche' l'alta pressione potrebbe schiacciare del mercurio aggiuntivo nella colonnina. Se il termometro e' non protetto, l'apparente temperatura letta sul ponte e' proporzionale alla temperatura ed alla pressione dove il termometro e' stato girato. Una coppia di termometri protetti e non protetti forniscono i valori della temperatura e della pressione dell'acqua alla quota dove i termometri sono stati rovesciati.

Le coppie di termometri a rovesciamento posizionate su bottiglie Nansen sono state la sorgente principale delle misure di temperatura in funzione della profondita' da circa il1900 al 1970.

Termometro al Platino
Questo e' lo standard per la temperatura. E' usato dai laboratori nazionali degli standard per interpolare tra i punti della scala pratica delle temperature. E' usato principalmente per calibrare gli altri sensori di temperatura.

Termistori
Un termistore e' un semiconduttore che ha una resistenza che varia con la temperatura. E' usato su strumenti ancorati e su quelli calati dalle navi sin da circa il 1970. Ha una risoluzione alta ed una accuratezza di circa ± 0.001°C quando e' stato calibrato con cura.

Temperatura del Secchio
La temperatura delle acque superficiali e' stata abitualmente misurata mettendo un termometro al mercurio in un secchio calato a mare, lasciandolo fermo ad una profondita' di un metro per pochi minuti fino a che il termometro andava all'equilibrio, allora era riportato a bordo e si doveva leggere i termometri prima che l'acqua del secchio avesse modo di cambiare. L'accuratezza e' intorno al 0.1°C. Questa era la piu' comune sorgente di misura diretta della temperatura superficiale.

Temperatura di Macchina
dell'acqua usata nella nave per raffreddare i motori e' stata abitualmente registrata. Gli errori sono dovuti alle strutture della nave che scaldano l'acqua prima che sia misurata. Cio' accade quando il registratore di temperatura non e' posizionato vicino al punto dello scafo dove l'acqua e' prelevata. L'accuratezza e' 0.5°-1°C.

Advanced Very High Resolution Radiometer
Lo strumento piu' comune per misurare la temperatura superficiale dallo spazio e' lo AVHRR (Advanced Very High Resolution Radiometer) Lo strumento e' stato installato su tutti i satelliti metereologici con orbita polare gestiti dal NOAA fin dal Tiros-N lanciato nel 1978.

Lo strumento e' stato originariamente progettato per misurare la temperatura delle nuvole e quindi la loro altezza. Lo strumento, comunque, aveva sufficiente accuratezza e precisione per essere presto usato per misurare le temperature regionali e globali della superfice marina.

Lo strumento e' un radiometro che converte la radiazione infrarossa in segnali elettrici. Include uno specchio che scansiona da bordo a bordo la traccia del satellite e riflette la radiazione della terra in un telescopio che concentra la radiazione sui rilevatori, questi, sensibili a diverse lunghezze d'onda covertono la radianza in segnali elettrici ed i circuiti elettronici digitalizzano e memorizzano i valori della radianza. Gli strumenti osservano una striscia larga 2700 km, centrata sulla traccia del satellite. Ogni osservazione lungo la scansione e' di un pixel di circa un kilometro di diametro vicino al centro della scansione che aumenta in diametro con la distanza dalla traccia del satellite.

I radiometri misurano la radiazione infrarossa emessa dalla superfice in cinque bande di frequenza: tre bande infrarosse: 3.55-3.99 µm, 10.3-11.3 µm, and 11.5-12.5 µm; una banda nel vicino infrarosso a 0.725-1.10 µm; e una banda nel visibile a 0.55-0.90 µm. Tutte le bande infrarosse includono la radiazione emessa dal mare e dal vapore acqueo nell'aria lungo la traiettoria dal satellite alla superfice della Terra. La banda a 3,7 µm e' la meno sensibile al vapore acqueo ed agli altri errori, ma funziona solo di notte perche' la luce solare emette in questa banda. Le due bande a lunghezza d'onda piu' grande a 10.8 µm e 12.0 µm sono usate per osservare la temperatura della superfice marina ed il vapore acqueo durante il giorno.

I dati con un una risoluzione di 1-km sono trasmessi direttamente alle stazioni a terra che vedono il satellite quando passa sulla stazione. Questo e' il modo "Local Area Coverage". I dati sono anche mediati per produrre osservazioni da pixel di 4x4 km. Questi dati sono registrati e trasmessi piu' tardi alle stazioni riceventi del NOAA. Questo e' il modo "Global Area Coverage".

La larghezza della striscia e' sufficientemente ampia da permettere la vista dell'intera Terra due volte al giorno, approssimativamente alle 09:00 ed alle 21:00 del tempo locale ????. Le aree ad alte latitudini possono essere osservate piu' spesso, fino ad otto volte al giorno. Gli errori piu' importanti sono dovuti a:

1. Nuuvole non risolte o non viste. Le nuvole grandi e spesse sono facilmente riconoscibili nelle immagini della temperatura dell'acqua, quelle sottili come i strati bassi (low stratus) e i cirri alti (high cirrus) producono molti piccoli errori che sono difficili o quasi impossibili da scoprire. Cosi' come le nuvole piu' piccole di 1km, come quelle dei cumuli degli alisei (trade-wind cumuli), sono difficili da scoprire. Tecniche speciali sono state sviluppate per rilevare le nuvole piccole. (Figure 6.12).
2. Il vapore acqueo, che assorbe parte dell'energia irradiata dalla superfice marina: il vapore acqueo riduce la temperatura apparente della superfice del mare. La differente influenza nei due canali 10.8 µm e 12.0 µm, permette alla differenza nei due segnali di essere usata per ridurre l'errore.
3. Gli aerosol, che assorbono la radiazione infrarossa. Irradiano quando sono nell'alta atmosfera. Gli aerosol stratosferici generati dalle eruzioni vulcaniche possono abbassare la temperatura fino a pochi gradi Celsius. Le particelle di polvere sopra l'Atlantico delle tempeste di sabbia del Shaara possono causare errori.
4. Errori dello strato esterno. La radiazione infrarossa vista dagli strumenti viene dallo strato di pochi millimetri (micrometers) della superfice marina. La temperatura in questo strato non e' esattamente la stessa di quella ad un metro sotto il pelo dell'acqua. Quando i venti sono deboli, possono differire di molti gradi (Emery and Schussel, 1989). Questi errori sono fortemente ridotti quando i dati AVHRR sono usati per interpolare le misure da nave della temperature marina.

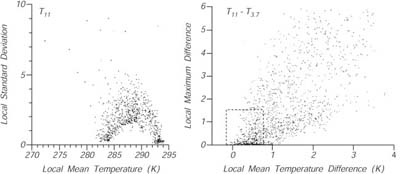Figura 6.12 L'influenza delle nuvole sulle osservazioni all'infrarosso. Sinistra: La deviazione standard della radianza da piccole aree parzialmente nuvolose ognuna contenete 64 pixel. I due piedi della distribuzione ad arco dei punti, corrisponde alla superfice marina ed alla temperatura delle nuvole. (Da Coakley e Bretherton (1982)). Destra: La differenza massima tra i valori locali di t11- t3.7 ed i valori medi locali delle stesse quantita'. I valori dentro il quadro tratteggiato indicano i pixel liberi da nuvole. t11 e t3.7 sono le temperature apparenti a 11.0 µm e 3.7 µm (dati da K. Kelly). Da Stewart (1985).

Le mappe di temperatura prodotte dalla "Local Area Coverage" delle regioni libere da nuvole mostrano variazioni della temperatura con la precisione di 0.1°C. Queste mappe sono utili per osservare fenomeni locali che includono caratteristiche prodotte dalle correnti locali. Figura 10.16 mostra queste caratteristiche a largo della costa della California.

Le mappe globali sono fatte dal U. S. Naval Oceanographic Office, che riceve i dati AVHRR globali direttamente dal NOAA's National Environmental Satellite, Data and Information Service in quasi tempo reale ogni giorno. I dati sono trattati con molta cura per rimuovere l'influenza delle nuvole, del vapore acqueo, degli aereosol e delle altre sorgenti di errori. I dati sono poi usati per produrre mappe globali tra ± 70° con una accuratezza di ± 0.6°C (May et a.,l 1998). Le mappe della superfice marina sono spedite al U.S. Navy ed al NOAA's National Centers for Environmental Prediction. In piu', l'ufficio produce giornalmente mappe della temperatura, globali di 100km e regionali di 14km.

Mappe Globali della Temperatura Superficiale del Mare
Mappe globali e mensili della temperatura superficiale dell'oceano sono prodotte dal National Centers for Environmental Prediction usando il metodo della interpolazione ottimale di Reynolds (1988, 1993, 1994). La tecnica mescola le misure della temperatura superficiale marina da navi e boe con i dati AVHRR trattati dal Naval Oceanographic Office in aree di 1° per un mese. Essenzialmente, i dati AVHRR sono usati per interpolare tra i dati di boe e navi, usando le informazioni dei precedenti campi di temperatura. Il range di accuratezza totale approssimativamente, va da ± 0.3°C nei tropici a ± 0.5°C vicino le "boundary current" occidentali nell'emisfero nord dove i gradienti di temperatura sono grandi. Le mappe sono disponibili da Novembre 1981. Figure 6.2 - 6.4 fatte dal NOAA usando la tecnica di Reynold.

Le mappe della temperatura media sono state fatte anche con i datiICOADS. I dati sono scarsamente distribuiti nel tempo e nello spazio eccetto per alcune aree dell'emisfero nord. Inoltre, Reynolds e Smith (1994) trovarono che i dati di temperatura misurati dalle navi hanno errori doppi di quelli misurati dalle boe e dai AVHRR. Quindi, i dati dallo spazio trattati da Reynolds sono piu' accurati e meglio distribuiti di quelli ICOADS.

Le anomalie della temperatura superficiale marina sono calcolate usando la temperatura del periodo 1950-979 calcolate dal dataset ICOADS integrate con quattro anni di dati da satellite 1982-1985 (Reynolds e Smith, 1995).

6.7 La Misura della Conducibilita'

La conducibilita' e' misurata posizionando elettrodi al platino in acqua marina e misurando la corrente elettrica che fluisce quando un voltaggio conosciuto e' applicato tra gli elettrodi. La corrente dipende dalla conducibilita', dal voltaggio e dal volume di acqua marina nel condotto tra gli elettrodi. Se gli elettrodi sono in un tubo di vetro non conduttivo, se il volume dell'acqua e' accuratamente conosciuto e se la corrente e' indipendente dagli altri oggetti vicini alla cella di conducibilita' (Figura 6.13). Allora, le migliori misure di salinita' dalla misura della conducibilita' danno la salinita' con un accuratezza di ±0.005.

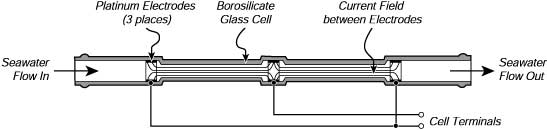Figura 6.13 Una Cella di Conducibilita'. La corrente elettrica fluisce nell'acqua marina tra gli elettrodi in un cilindro di vetro borosilicato lungo 191 mm con un diametro interno di 4 mm. Le linee del campo elettrico (linee solide) sono confinate all'interno della cella in questa figura, rendendo le misure di conducibilita' (e la calibrazione dallo strumento) indipendenti dagli oggetti vicini alla cella. Questa e' la cella usata per misurare la conducibilita' e la salinita' (vedi anche Figura 6.15). Da Sea-Bird Electronics Inc..

Prima che le misure di conducibilita' fossero ampiamente usate, la salinita' era misurata usando la tritazione chimica dei campioni di acqua con sali d'argento. La migliore misura della salinita' con la tritazione da' la salinita' con una accuratezza di ±0.02.

Le misure di campioni individuali di salinita' sono calibrate usando standard di acqua di mare. Studi di lungo periodo dell'accuratezza usano dati da misure di masse d'acqua profonde di salinita' nota e stabile. Per esempio, Saunders (1986), ha notato che la temperatura e' relazionata con molta precisione alla salinita' di grandi volumi di acqua contenuti nei bacini profondi dell'Atlantico di nord-ovest sotto il flusso che esce dal Mediterraneo. Ha usato la consistenza delle misure di temperatura e salinita' fatte in molte stazioni idrografiche in quell'area, per stimare la accuratezza delle misure di temperatura, di salinita' e di ossigeno disciolto. Ha concluso che le misure piu' precise fatte fino ? al 1970 hanno una accuratezza di 0.005 per la salinita' e di 0.005°C per la temperatura. La maggiore sorgente di errori nella salinita' viene dall'errore nella determinazione dell'acqua standard usata per calibrare le misure di salinita'.

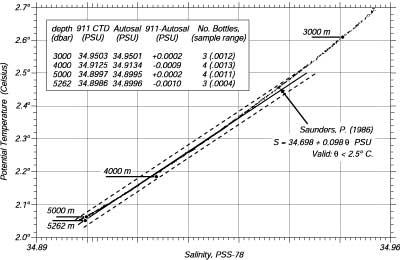
Gouretski a Jancke (1995) stimarono la accuratezza delle misure di salinita' come funzione del tempo. Usando misure di alta qualita' da 16,000 stazioni oceanografiche del sud Atlantico dal 1912 to 1991, loro stimarono la accuratezza dal tracciare la salinita' come una funzione della temperatura, usando tutti i dati raccolti sotto i 1500m in dodici regioni per ogni decade dal 1920 al1990. Una figura della accuratezza come funzione del tempo dal 1920 mostra consistenti miglioramenti nell' accuratezza dal 1950 (Figura 6.14). Le misure recenti di salinita' sono le piu' accurate. La deviazione standard dei dati di salinita' moderni raccolte in sud Atlantico dal 1970 al 1993 aggiustate come descritto da Gouretski e Jancke (1995) e' 0.0033. Gli strumenti piu' recenti come il modello "911 plus" della Sea-Bird Electronics ha una accuratezza di 0.005psu senza aggiustamenti. Una comparazione accurata delle misure di salinita' a 43° 10'N, 14° 4.5'W tra i dati del 911 Plus e i dati storici raccolti da Saunders (1986) da' una accuratezza di 0.002 psu(Figura 6.15).

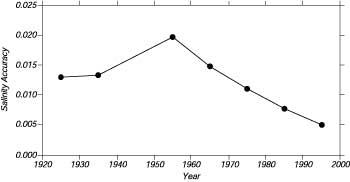Figura 6.14. Deviazioni standard delle misure di salinita' a profondita' sotto i 1500 m del sud Atlantico dal 1920 al 1993. Ogni punto e' la media dei dati raccolti per la decade centrata sul punto. Il valore del 1995 e' una stima dell'accuratezza degli misure recenti. Dalla Tabella 1 di Gouretski e Jancke (1995).

Figura 6.15. Resultati della prova del CTD 911plus della Sea-Bird Electronics nelle acque profonde dell'Atlantico settentrionale del 1992. I dati furono raccolti a 43.17°N e 14.08°W dalla R/V Poseidon. Da Sea-Bird Electronics (1992).

6.8 La Misura della Pressione

La pressione e' abitualmente misurata in molti tipi differenti di strumenti. L'unita' internazionale (SI) della pressione e' il pascal (Pa), ma gli oceanografi normalmente riportano la pressione in decibars (dbar), dove:

poiche' la pressione in decibar e' quasi esattamente uguale alla profondita' in metri. Cosiche' 1000 dbar e' la pressione alla profondita' di 1000 m.

Strain Gage
Questo e' il piu' semplice ed economico strumento, ed e' largamente usato. L'accuratezza e' circa ±1%.

Vibratron
Misure di pressione molto piu' accurate possono esse fatte misurando la naturale frequenza di un filo al tungsteno vibrante e in un campo magnetico e tirato tra due diaframmi che chiudono i due lati di un cilindro. La pressione distorce i diaframmi, che cambiano la tensione del filo e la sua frquenza. La frequenza puo' essere misurata dal cambiamento del voltaggio indotto dal filo che vibra nel campo magnetico. L'accuratezza e' circa del ±0.1%, o migliore se la temperatura e' controllata. La precisione e' 100-1000 volte migliore dell'accuratezza. Lo strumento e' usato per individuare piccoli cambiamenti di pressione a grandi profondita'. Snodgrass (1968) ottenne una precisione equivalente ad un cambiamento profondita' di ±0.8 mm ad una quota di 3 km.

Cristalli di Quarzo
Misure molto accurate di pressione possono essere fatte anche misurando la naturale frequenza di un cristallo di quarzo tagliato per avere una dipendenza piccola dalla temperatura. La migliore accuratezza e' ottenuta quando la temperatura del cristallo e' tenuta costante. La accuratezza e' ±0.015%; e la precisione e' ±0.001% dei valori di fondo scala.

Quartz Bourdon Gage
L'accuratezza e la stabilita' sono comparabili a quelle dei cristalli al quarzo. Anche questo e' usato per misure di pressione a lungo termine nel mare profondo.

6.9 La Misura della Temperatura e della Salinita' con la Profondita'

La temperature, la salinita', e la pressione sono misurati come funzione della profondita', usando vari strumenti o tecniche, e la densita' e' calcolata dalle misure.

Batitermografo (BT)
Un congegno meccanico che misura la temperatura verso la profondita' su un lastrina di vetro affumicato. Lo strumento e' stato largamente usato per mappare la struttura termale della parte alta dell'oceano, includendo la profondita' del "mixed layer" prima di essere rimpiazzato dal batitermografo a perdere negli anni 70.

Batitermografo a Perdere XBT (eXpendebale BT)
Un congegno elettronico che misurava la temperatura verso la profondita' usando un termistore su un peso a caduta libera. Il termistore e' connesso The thermistor is connected ad un ohm-metro sulla nave da un sottile filo di rame che si svolge dal peso e dalla nave che si muove. L'XBT e' attualmente lo strumento piu' usato per misurare la struttura termale della parte superiore dell'oceano. Approssimativamente ogni anno ne sono lanciati 65 000.

Il peso affusolato cade lungo la colonna d'acqua con velocita' terminale costante. Cosi che, la profondita' puo' essere calcolata dal tempo di caduta con una accuratezza del ±2%. L'accuratezza della temperatura e' ±0.1°C. E, la risoluzione verticale e' tipicamente di 65 cm. A seconda del modello usato le sonde raggiungono la profondita' da 200 m a 1830 m.

Bottiglie Nansen
(Figura 6.16) Calate da navi ferme sulle stazioni oceanografiche. Le stazioni Hydrographic sono posizionate nei punti dove gli oceanografi misurano le propieta' dell'acqua, dalla superfice al fondo, oppure al fondo, usando strumenti calati dalla nave. Di solito 20 bottiglie sono attaccate ad intervalli di poche centinaia di metri ad un cavo calato da un lato della nave. La distribuzione sulla profondita' e' scelta in modo da posizionare molte bottiglie nelgli strati superiori della colonna d'acqua, dove i gradienti di temperatura nella verticale sono piu' grandi. Un termometro a rovesciamento protetto dalla pressione per misurare la temperatura, e' attaccato ad ogni bottiglia insieme con un termometro a rovesciamento non protetto per misurare la profondita'. Le bottiglie contengono un tubo con rubinetti ad ogni estremita' per raccogliere acqua di mare alla profondita voluta.

Dopo che le bottiglie sono state attaccate al cavo ed il tutto e' stato calato alle profondita' scelte, un peso (messaggero) e' lasciato cadere lungo il cavo. Il peso fa' scattare un meccanismo in ogni bottiglia, la bottiglia si capovolge, rovesciando i termometri, chiudendo le valvole, intrappolando l'acqua nel tubo e rilasciando un altro peso, che fa' scattare la bottiglia sottostante, e cosi' via fino alla bottiglia piu' profonda. Quando tutte le bottiglie sono chiuse, il tutto viene recuperato. Un calamento ed il recupero tipicamente dura alcune ore.

Figura 6.16 Left: Un CTD pronto per essere calato dalla poppa di una nave. From Davis (1987). Right: Una bottigla Nansen prima (I), durante (II), e dopo (III) il rovesciamento. Entrambi gli strumenti sono in scala. Da Defant (1961: 33).

CTD
A partire dal 1960, gli strumenti meccanici sulle bottiglie Nansen furono rimpiazzati da uno strumento elettronico, chiamato CTD, che misurava la condicibilita', la temperatura e la profondita' (Figure 6.16). Quando lo strumento veniva calato da una nave, le misure erano registrate dentro lo strumento stesso oppure nella nave. La temperatura e' di solito misurata da un termistore; la condicibilita' da una induzione; la pressione da un cristallo di quarzo. Gli ultimi strumenti hanno le accuratezze riassunte in Tabella 6.2.

6.10 La Luce nell'Oceano e l'Assorbimento della Luce

La luce solare nell'Oceano e' importante per molte ragioni. Riscalda l'acqua marina, e gli strati superficiali; fornisce l'energia richiesta dal fitoplankton; e' usata per la navigazione dagli animali vicini alla superfice; e la luce subsuperficiale riflessa e' usata per mappare dallo spazio la concentrazione della clorofilla.

La luce viaggia nell'Oceano ad una velocita' eguale a quella nel vuoto diviso l'indice di rifrazione, (n), che e' tipicamente n = 1.33. Quindi la velocita' nell'acqua e' circa 2.25×10⁸ m/s. Poiche' la luce viaggia piu' lenta nell'acqua che nell'aria, ??? un po' di luce e' riflessa alla superfice marina. ??? Per la luce allo zenith sopra il mare, la riflettivita' e' (n - 1)2/(n + 1)2. Per l'acqua di mare, la riflettivita' e' 0.02 = 2%. Percio', molta luce solare che raggiunge la superfice del mare e' trasmessa dentro, poca e' riflessa. Questo significa che la luce solare incidente al mare nei tropici e' principalmente assorbita sotto la superfice del mare.

Il tasso al quale la luce solare e' attenuata determina la profondita' che e' ancora illuminata e riscaldata dal sole. L'attenuazione e' dovuta all'assorbimento da pigmento e dalla dispersione di particelle e molecole. L'attenuazione dipende dalla lunghezza d'onda. La luce blu e' assorbita meno, Quella rossa e' assorbita molto. L'attenuazione per unita' di distanza e' proporzionale alla radianza o all'irraggiamento della luce:

(6.12)

dove x e' la distanza lungo il raggio, c e' un coefficiente di attenuazione (Figura 6.17), e I e' l' irradianza ??? irradiance or irradiance ???.

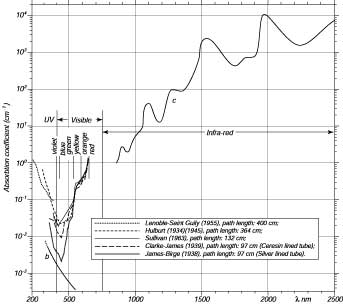Figura 6.17 Coefficiente di Assorbimento per acqua pura in funzione della lunghezza d'onda λ della radiazione. Ridisegnato da Morel (1974: 18, 19). Vedi Morel (1974) per i riferimenti.

Radianza e' la potenza per unita' di area per angolo solido. E' utile per descrivere l'energia in un raggio di luce proveniente da una particolare direzione. Talvolta vogliamo sapere quanta luce raggiunge una certa profondita' marina senza riguardo alla direzione che ha. In questo caso usiamo irradianza, che e' la potenza per unita' di superfice.

Se il coefficiente di assorbimento e' costante, l'intensita' della luce decresce esponenzialmente con la distanza.

dove I₁e' l'originale radianza o irradianza della luce, e I₂ e' la radianza o irradianza della luce dopo l'assorbimento.

La Chiarezza dell'acqua di mare(Torbidita' ??) L'acqua marina nel mezzo dell'oceano e' molto pulita- piu' chiara dell'acqua distillata. Queste acque sono molto profonde, cobalto,blue - quasi nero. Tanto che la forte corrente che fluisce verso nord a largo del Giappone, portando acque molto pulite dal Pacifico centrale alle alte latitudini e' conosciuta come la "Corrente Nera", o "Kuroshio" in giapponese. Le acque piu' chiare dell'oceano sono dette acque di Type I da Jerlov (Figura 6.18).L'acqua e' cosi' chiara che il 10% della luce transmessa sotto la superfice marina raggiunge la profondita' di 90m.

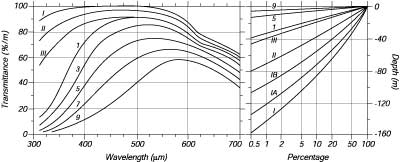Figura 6.18 Sinistra: Attenuazione della luce solare in mare in % per metro in funzione della lunghezza d'onda. I: acqua oceanica estremamente pura; II: acqua torbida tropicale-subtropicale; III: acqua delle medie-latitudini; 1-9: acque costiere di crescente torbidita'. L'angolo incidente e 90° per i primi tre casi, 45° per gli altri. Destra: Percentuale della luce a 465nm che raggiunge le profondita' indicate per gli stessi tipi di acque. Da Jerlov (1976).

Nei sub-tropici ed alle medie latitudini vicini alla costa, l'acqua marina contiene piu' fitoplankton delle acque molto chiare del centro oceano. I pigmenti di clorofilla del fitoplankton assorbono la luce, e le piante stesse disperdono la luce. Insieme i processi cambiano il colore del mare come viene visto da un osservatore che sta guardando dall'alto lungo la verticale.Le acque molto produttive, quelle con alte concentrazioni di fitoplankton, appaiono blu-verdi oppure verdi (Figura 6.19). Nei giorni chiari il colore puo' essere osservato dallo spazio. Questo permette agli scanner del colore del mare (ocean-color), come quelli sul SeaWiFS, di mappare la distribuzione del fitoplankton su grandi aree.

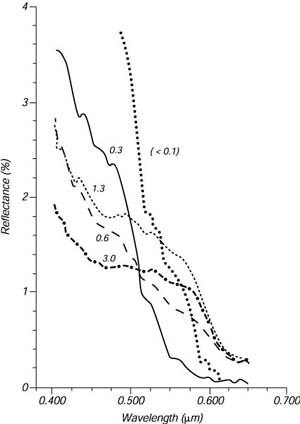Figura 6.19 Spettro della Riflettanza (Spectral reflectance) dell'acqua marina osservata da un aereo che vola a 305 m sopra le acque a differenti colori dell'Atlantico di nord ovest. I valori numerici sono le concentrazioni medie di clorofilla nella zona eufotica (con luce solare) in unita' di mg/m3. La riflettanza e' per luce polarizzata verticalmente osservata a 53° dell'angolo di Brewster. Questo angolo minimizza la luce del cielo riflessa ed enfatizza la luce da sotto il pelo dell'acqua. Da Clarke, Ewing, e Lorenzen (1970).

Come la concentrazione di fitoplankton aumenta, la profondita' del mare dove la luce del sole e' assorbita diminuisce. Le acque tropicali e di media-latitudine piu' torbide sono classificate come ?? classi.ed ?? II e III da Jerlov (Figura 6.18). Cosi' la profondita' dove la luce solare riscalda le acque dipende dalla produttivita' delle stesse acque. Questo complica il calcolo del riscaldamento solare dello strato mescolato (mixed layer).

Le acque costiere sono molto meno chiare di quelle al largo. Queste sono i tipi 1–9 di acqua mostrati in Figura 6.18. Contengono pigmenti di origine terrestre talvolta chiamati gelbstoffe, che vuole dire "roba" gialla, acque fangose dei fiumi, e fango agitato dalle onde in acqua poco profonde. Pochissima luce penetra solo pochi metri in queste acque.

La Misura della Clorofilla dallo Spazio
Il colore dell'oceano, e quindi la concentrazione di clorofilla negli strati alti del mare e' stato misurato dal Coastal Zone Color Scanner portato dal satellite Nimbus-7 lanciato nel 1978 e dal Sea-viewing Wide Field-of-view Sensor (SeaWiFS) portato dal SeaStar, lanciato nel 1997. Quest'ultimo strumento misura la upwelling radianza in otto bande di lunghezza d'onda tra 412nm a 856nm.

Molta della radianza di upwelling vista dal satellite proviene dall'atmosfera. Solo circa il 10% viene dalla superfice marina. Sia le molecole di aria, sia gli aereosol disperdono la luce; e tecniche molto accurate sono state sviluppate per rimuovere l'influenza dell'atmosfera.

La radianza totale L_t ricevuta da uno strumento nello spazio e':

dove λ_i e' la lunghezza d'onda della radiazione nella banda misurata dallo strumento, L_W e' la radianza emessa dalla superfice marina, L_r e' la radianza dispersa dalle molecole, chiamata radianza di Rayleigh, L_a e' la radianza dispersa dagli aerosol, e t e' la trasmittanza dell'atmosfera. L_r puo' essere calcolata dalla teoria; e L_apuo' essere calcolata dalla quantita' di luce rossa ricevuta dallo strumento perche' pochissima luce rossa e' riflessa dall'acqua. Infine L_W puo' essere calcolata dalla radianza misurata dal satellite.

La concentrazione di Clorofilla nella colonna d'acqua e' calcolata dal rapporto di L_W a due frequenze. Usando i dati del Coastal Zone Color Scanner, Gordon et al., (1983) propose

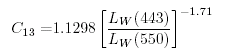	(6.15a)
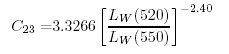	(6.15b)

dove C e' la concentrazione di clorofilla negli strati superficiali in mg pigment/m³, e L_W(443), L_W(520), e L_W(550) e' la radianza alla lunghezza d'onda di 443 nm, 520nm, and 550nm. C₁₃ e' usata quando C₁₃ ≤ 1.5 mg/m³; altrimenti C₂₃ e' usata.

Questa tecnica e' usata per calcolare la concentrazione di clorofilla entro un fattore del 50% su un intervallo ampio di concentrazioni: da 0.01 mg/m³ a 10 mg/m³.

6.11 Concetti Importanti

1. La Densita' dell'oceano e' determinata dalla temperatura, dalla salinita' e dalla pressione. pressure.
   
   
2. I cambiamenti di Densita'nell'ocean sono molto piccoli, e gli studi delle masse di acqua e delle correnti richiedono misure di densita' con una accuratezza di 10 parti per milione.
   
   
3. La densita' non e' misurata, e' calcolata dalle misure di temperatura, di salinita' e di pressione usandol'equazione di stato dell'acqua di mare.
   
   
4. Calcoli accurati della densita' richiedono definizioni precise della temperatura e della salinita', e una accurata equazione di stato.
   
   
5. La salinita' e' difficile da definire e da misurare. Per evitare le difficolta' , gli oceanografi usano la conducibilita' invece della salinita'. Misurano la conducibilita' invece della Salinita' e calcolano la densita' dalla temperatura, dalla conducibilita' e dalla pressione.
   
   
6. Uno strato mescolato a temperatura e salinita' costante e' di solito trovato nei primi 100m del mare. La prfondita' e' determinata dalla velocita' del vento e del flusso di calore attraverso la superfice marina.
   
   
7. Per comparare temperature e densita' delle masse di acqua a differenti profondita' dell'oceano, gli oceanografi usano temperature e densita' potenziali, che rimuovono completamente l'influenza della pressione, specialmente sulla densita'.
   
   
8. Porzioni di acqua sotto il "mixed layer" si muovono lungo superfici neutrali.
   
   
9. La temperatura superficiale del mare e generalmente misurata usando il secchio oppure le temperature di macchina. Le mappe globali di temperatura combinano queste osservazioni con quelle della radiazione infrarossa della superfice marina, misurate da un satellite AVHRR.
   
   
10. La temperature e la conducibilita' sono generalmente misurate digitalmente come una funzione di pressione usando un CTD. Prima del 1960-1970, la salinita' e la temperatura erano misurate a circa 20 quote usando le bottiglie Nansen, calate con un cavo da una nave. Le bottiglie portano termometri a rovesciamento che misurano e registrano la temperatura e la profondita', e riportano a bordo un campione di acqua da cui puo' essere determinata la salinita'.
    
    
11. La luce e' rapidamente assorbita nel mare. Il 95% della luce solare e' assorbita nei primi 100m dell'acqua di mare piu' chiara. La luce solare molto difficilmente penetra piu in profondita' di pochi metri in acque costiere torbide.
    
    
12. Il Fitolankton cambia i colori dell'acqua di mare, ed il cambiamento del colore puo' essere osservato dallo spazio. I colori dell'acqua sono usati per misurare le concentrazioni di fitoplankton dai satelliti.