Capitolo 8 - Equazioni del Moto con la Viscosita'
|
Capitolo 8
|
Quasi ovunque nell'Oceano e nell'Atmosfera l'attrito e' abbastanza piccolo, e possiamo sicuramente assumere che il flusso e' senza attrito. Ai confini, l'attrito, in forma di viscosita', diventa importante. Questo sottile strato viscoso e' detto uno strato di confine (boundary layer). Dentro lo strato, la velocita' rallenta dai valori tipici dell'interno fino a zero al confine solido. Se il confine non e' solido, allora lo strato di confine e' uno strato sottile di velocita' che cambiano rapidamente: le velocita' in un lato del confine cambiano per essere uguali a quelle dell'altro lato. Per esempio, c'e' uno strato di confine al fondo dell'atmosfera, lo strato di confine planetario descritto nel capitolo 3. Nello strato di confine planetario, la velocita' va' da molti metri al secondo nella libera atmosfera a decine di centimetri al secondo nel mare. Sotto la superfice, un'altro strato di confine, lo strato di Ekman descritto nel Capitolo 9, eguaglia il flusso della superfice con quello piu' profondo.
In questo capitolo considero il ruolo dell'attrito nel flusso dei fluidi, e la stabilita' dei flussi ai piccoli cambiamenti nella velocita' e nella densita'.
8.1 L'Influenza della Viscosita'
Nell'ultimo capitolo ho scritto la componente x dell'equazione del momento nella forma (7:12a):
|
|
(8.1) |
dove Fx era una forza di attrito per unita' di massa. Ora possiamo considerare la forma di questo termine se e' dovuto alla viscosita'.
Le molecole in un fluido vicino ad un confine solido qualche volta sbattono sul confine gli trasferiscono momento (Figure 8.1). Le molecole piu' lontane dal confine urtano con le molecole che hanno colpito il confine, trasferendo ulterioriormente il cambio nel momento all'interno del fluido. Questo trasferimento del momento e' la viscosita' molecolare. Le molecole, comunque, viaggiano soltanto per micrometri tra le collisioni, ed il processo e' molto inefficiente per trasferire momento anche per pochi centimetri. La viscosita' molecolare e' molto important soltanto entro pochi millimetri dal confine.
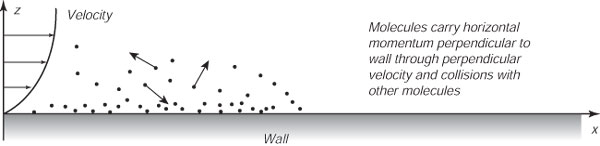 |
| Figura 8.1 Le molecole che collidono sul muro e fra loro trasferiscono momento dal fluido al muro, rallentando la velocita' del fluido. |
La viscosita' molecolare e' il rapporto dello sforzo Tx tangenziale al confine di un fluido e la deformazione del fluido al confine. In tal modo lo sforzo ha la forma di:
|
|
(8.2) |
per il flusso nel piano ( x, z ) entro pochi millimetri dalla superfice, dove ν e' la viscosita' cinematica molecolare. Tipicamente ν = 10-6m2/s per acqua a 20°C.
Generalizzando la (8.2) in tre dimensioni porta al tensore dello sforzo, che da' le nove componenti dello sforzo ad un punto del fluido, includendo la pressione, che e' uno sforzo perpendicolare, e gli sforzi di deformazione. Una derivazione del tensore dello sforzo e' oltre lo scopo di questo libro, ma potete trovare i dettagli in Lamb (1945: §328) oppure Kundu (1990: p. 93). Per un fluido incompressibile, la forza di attrito per unita' di massa della (8.1) prende la forma di:
|
|
(8.3) |
8.2 Turbolenza
Se la viscosita' molecolare e' importante solo su distanze di pochi millimetri, e se non e' importante per molti flussi oceanici, naturalmente se non si e' uno zooplankton che cerca di nuotare nell'oceano, come allora e' l'influenza di un confine trasferita all'interno del flusso? La risposta e': attraverso la turbolenza.
La turbolenza deriva dai termini non-lineari dell'equazione del momento (u ∂u/∂x, etc.). L'importanza di questi termini e' data da un numero non-dimensionale Il numero di Reynolds Re, che e' il rapporto dei termini non-lineari sui termini viscosi:
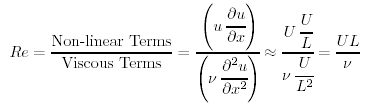 |
(8.4) |
dove, U e' la tipica velocita' del flusso e L e' la tipica lunghezza che descrive il flusso. Siamo liberi di considerare qualunque U, L possa essere tipica del flusso. Per esempio L puo' essere una tipica distanza perpendicolare alla corrente oppure lungo la corrente. Valori tipici vicino alla superfice sono U = 0.1m/s e L = 1 milione di metri, cosi' Re = 1011. Poiche' i termini non-lineari sono importanti se Re > 10-1000, e certamente sono importanti in un oceano. L'Oceano e' turbulento.
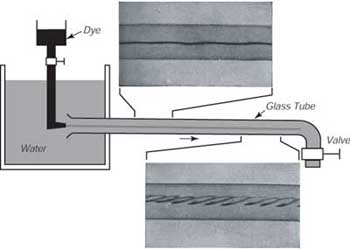
Il numero di Reynolds e' cosi' chiamato dopo che Osborne Reynolds (1842-1912) condusse esperimenti nel tardo 19-esimo secolo per capire la turbolenza. In un famoso esperimento (Reynolds 1883), inietto un colorante nell'acqua che fluiva a varie velocita' attraverso un tubo (Figura 8.2). Se la velocita' era piccola, il flusso era regolare. Questo e' detto flusso laminare. A velocita' piu elevate, il flusso diventava irregolare e turbolento. La transizione avviene a Re = VD/ν ≈ 2000, dove V e' la velocita' media nel tubo, e D e' il diametro del tubo.
| Figura 8.2 L'apparato di Reynolds per studiare la transizione alla turbolenza nel condotto forzato, con le foto (a sinistra) del flusso quasi laminare ed (a destra) di quello turbolento nel condotto trasparente molto simile a quello usato da Reynolds. Da Binder (1953). |
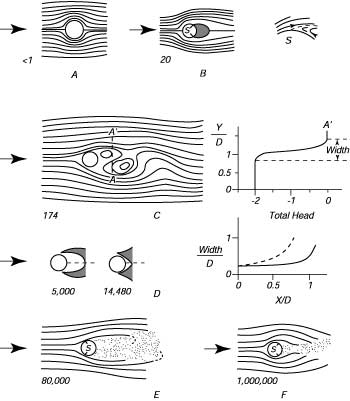
Come il numero di Reynolds aumenta sopra alcuni valori critici, il flusso diventa sempre piu' turbolento. Notare che la forma del flusso e' in funzione del numero di Reynold. Tutti i flussi con la stessa geometria e lo stesso numero di Reynolds hanno la stessa forma. Cosi' il flusso in tutti i cilindri circolari, da un 1mm o da 1m di diametro, sono uguali come il flusso in alto della figura 8.3 se il numero di Reynolds e' 20. Inoltre, lo strato di confine e' ristretto ad uno strato molto sottile sulle pareti del cilindro, in uno strato troppo sottile per essere visto nella figura.
| Figura 8.3 Il flusso intorno ad un cilindro circolare in funzione del numero di Reynolds tra uno ed un milione. Da Richardson (1961). I flussi appropriati sono: A—uno stuzzicadenti con velocita' di 1 mm/s; B—un dito con 2 cm/s; F—una mano fuori il finestrino di un auto che corre a 60 mph. Tutti i flussi hanno lo stesso numero di Reynolds con le stesse linee di corrente. Il flusso intorno al cilindro di 10 cm di diametro ad una velocita' di 1 cm/s e' uguale a quello di 10 cm/s intorno ad un cilindro di 1 cm di diametro perche' in entrambi i casi Re = 1000. |
Sforzi Turbolenti: Gli Sforzi di Reynolds
Prandtl, Karmen ed altri che studiarono la meccanica dei fluidi all'inizio
del 1900', ipotizzarono che le particelle del fluido in un flusso turbolento
giocano lo stesso ruolo nel trasferire il momento dentro al flusso come le
molecole giocano in un flusso laminare. Il lavoro porto' all'idea di sforzi turbolenti.
Per vedere come questi sforzi possono agire, consideriamo l'equazione del momento per un flusso con una componente del flusso media (U, V, W) ed una turbolenta (u, v, w):
|
u = U + u' ; v = V + v' ;
w = W + w' ; p = P + p' |
(8.5) |
dove il valore medio U e' calcolato da un tempo ed uno spazio medio:
|
|
(8.6) |
I termini non-lineari dell'equazione del momento possono essere scritti:
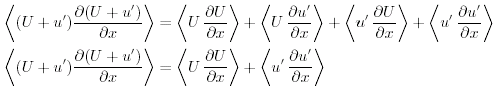 |
(8.7) |
La seconda equazione deriva dalla prima perche' <U ∂u'/∂x> = 0 e < u' ∂U/∂x> = 0, che segue dalla definizione di U: <U ∂u'/∂x> = U∂<u'>/∂x = 0.
Usando la (8.7), l'equazione di continuita' si divide nelle due equazioni:
|
|
(8.8a) |
|
|
(8.8b) |
La componente x dell'equazione del momento diventa:
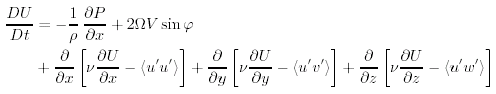 |
(8.9) |
Cosi' la forza addizionale per unita' di massa dovuta alla turbolenza e':
|
|
(8.10) |
I termini ρ < u 'u' >, ρ < u' v' >, e ρ < u' w' > trasferiscono momento verso est (ρ u) nelle direzioni x, y, e z. Per esempio, il termine ρ < u' w' > fornisce il trasporto del momento verso est su un piano orizzontale. Poiche' trasferiscono momento, e poiche' furono derivati da Osborne Reynolds, sono chiamati Sforzi di Reynolds (Reynolds Stresses).
8.3 Calcolo degli Sforzi di Reynolds
Gli sforzi di Reynolds come ∂<u' w' >/∂z sono chiamati sforzi virtuali (cf. Goldstein, 1965: §69 & §81) perche' assumiamo che essi giochino lo stesso ruolo dei termini viscosi delle equazioni del moto. Per procedere ulteriormente, abbiamo bisogno di valori o forme funzionali degli sforzi di Reynolds. Sono stati usati molti approcci.
Per Analogia con la Viscosita' Moleculare
Torniamo al semplice esempio mostrato in Figura 8.1, che mostra uno strato
di confine sopra un superfice uniforme sul piano x, y. Ora assumiamo
che il flusso sopra alla superfice sia turbolento. Questo e' un tipo di flusso con strato
limite molto comune, e inoltre e' un tipo di flusso che descriveremo molte volte nei
prossimi capitoli. Potrebbe essere il vento che soffia sopra la superfice marina
oppure lo strato limite del fondo di un Oceano o ancora il flusso dello strato mescolato
alla superfice marina.
Per il flusso sopra un confine, assumiamo che esso sia costante nella direzione x, y, e che le propietà statisticche del flusso variano solo nella direzione z, e che il flusso sia stazionario (cioe' costante). Quindi ∂ /∂t = ∂ /∂x = ∂ /∂y = 0, e la (8.9) può essere scritta:
 |
(8.11) |
Ora assumiamo, in analogia alla (8.2)
|
|
(8.12) |
dove Az è una viscosità vorticosa che rimpiazza la viscosita' moleculare nella (8.2). Con questa assunzione,
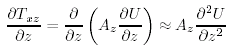 |
(8.13) |
dove abbiamo posto che Az è constante or lentamente variabile nella direzione z allora ∂U/ ∂z. Piu' tardi assumeremo che Az>> z.
L'equazioni del momento in x e y per uno strato di confine omogeneo turbolento e stazionario sopra o sotto una superfice orizzontale sono:
|
|
(8.14a) |
|
|
(8.14b) |
dove f = 2 Ω sin(φ) è il parametro di Coriolis, e abbiamo cancellato il termine della viscosita' molecolare perche' è molto piu' piccolo della viscosita' vorticosa turbolenta. Da notare, che la (8.14b) segue da una derivazione simile dalla componente y dell'equazione del momento. Avremo bisogno della (8.14) quando descriviamo il flusso vicino la superfice.
L'assunzione che una viscosità vorticosa Az può essere usata per relazionare gli sforzi di Reynolds al flusso medio viene a proposito per descrivere il flusso vicino alla superfice orizzontale dove U è in funczione della distanza z dalla superfice, e W, la velocità media perpendicolare alla superfice e' zero (Vedi il riquadro Strato di Confine Turbolento sopra un Piano Piatto). Questo è l'approccio, descritto per primo nel 1925 da Prandtl e poi da altri, che introdusse il concetto di strato di confine. Per favore notare che un valore di Az non può essere ottenuto dalla teoria. Invece, può essere calcolato dai dati raccolti nella galleria del vento oppure misurati negli strati limite del mare. Vedi Hinze (1975, §5-2 e §7-5) e Goldstein (1965: §80) per approfondimenti della teoria del flusso turbolento vicino una superfice orizzontale.
|
Lo Strato Limite Turbolento Sopra una Superfice Orizzontale La teoria per la distribuzione della velocita media in uno strato limite turbolento sopra un piano piatto e' stata segnalata independentemente da G.I.Taylor (1886-1975), L. Prandtl (1875-1953), e T. von Karman (1818-1963) dal 1915 al 1935. La Teoria empirica, talvolta chiamata la Teoria della lunghezza di mescolamento predice bene il profilo della velocita' media vicino al limite. Cosa che a noi interessa particolarmente, predice il flusso medio dell'aria sopra il mare. Di seguito troviamo una versione semplificata della teoria applicata alla superfice liscia. Cominciamo assumendo che il flusso medio nello strato di confine è stazionario e che varia soltanto nella direzione z. Entro pochi millimetri dal confine, la frizione è importante e la (8.2) ha la soluzione
e la velocità media varia linearmente con la distanza dal confine. Generalmente la (8.16) è scritta in forma a-dimensionale:
dove u*2 ≡ Tx/ ρ è la velocità frizionale. Lontano dal confine, il flusso è turbolento, e l'attrito molecolare non è importante. In questo regime, possiamo usare la (8.12), e
Prandtl e Taylor assumono che i grandi vortici (eddy) sono piu' (.. effective in mixing momentum ..) dei piccoli vortici, e quindi Az ought to vary with distance from the wall. Karman assunse che questo ha la particolare forma funzionale Az = kzu*, dove k è una costante senza dimensioni. Con questa assunzione, l'equazione per il profilo di velocita' medio diventa
Poichè U è una funzione soltanto di z, possiamo scrivere che dU = u*/(kz) dz, che ha la seguente soluzione
dove z0 è la distanza dal confine e che la velocita' và a zero. Per il flusso di aria sopra l'Oceano, k = 0.4 e z0 e' dato dalla relazione di Charnock's (1955) z0 = 0.0156 u*2/g. La velocita' media nello strato limite ell'atmosfera propio sopra la surface descritta nel §4.3 e' in buon accordo con il profilo logaritmico della (8.20), come appare essere la velocitità media nei primi metri propio sotto la superfice marina. Ed ancora, usando la(4.1) della definitione della velocita' di attrito, allora usando la (8.20) fornisce la forma di Charnock del coefficiente di attrito in funzione della velocita' del vento nella figura 4.6 |
La teoria di Prandtl basata sull'assunzione della (8.12) lavora bene soltanto dove l'attrito è molto piu' grande della forza di Coriolis. Questo è vero per il flusso di aria entro dieci metri dalla superfice marina e per il flusso di acqua entro pochi metri dalla superfice. L'applicazione della tecnica ad altri flussi dell'Oceano è meno chiara. Per esempio, il flusso dello strato limite a profondità sotto circa dieci metri è meno ben descritto dalla teoria classica della turbolenza. Tennekes e Lumley (1970: 57) scrivono:
La lunghezza di mescolamento ed i modelli di viscosita' vorticosa dovrebbero essere usati soltanto per generare espressioni analitiche degli sforzi di Reynolds e i profili medi di velocita' se questi sono voluti per appromean-velocity profile if those are desired for curve fitting purposes in turbulent flows characterized by a single length scale and a single velocity scale. L'uso della teoria della lunghezza caratteristica di mescolamento in flussi turbolenti le cui leggi di scala sono sconosciute dovrebbero essere evitato a priori.
Problemi con l'approccio della viscosita' vorticosa:
1. Eccetto che in strati limite con pochi metri di spessore, i flussi geofisici possono essere influenzati da parecchie scale caratteristiche. Per esempio, nello strato limite atmosferico sopra il mare, almeno tre scale possono essere importanti:
i) l'altezza sopra il livello marino z,
ii) la scala L di Monin-Obukhov discussa nella §4.3, e
iii) la velocità tipica U divisa per il parametro di Coriolis U / f.2. Le velocità u', w' sono una propietà del fluid, mentre Az e' una propietà del flusso;
3. I termini della viscosità vorticosa non sono simmetrici:
|
< u' v' > = < v' u'>; ma
|
|
|
Dalla Teoria Statistica della Turbolenza
Gli stress di Reynolds possono essere calcolati da varie teorie che collegano
< u 'u' > alle correlazioni di ordine piu' alto nella forma di < u' u' u' >.
Il problema allora diventa: Come calcolare i termini di ordine piu' alto? Questo è la
chiusura del problema nella turbolenza. Non c'è una soluzione general,
ma l'approccio porta utili comprensioni di alcune forme di turbolenza come la turbolenza
isotropica verso il basso della griglia nella galleria del vento (Batchelor 1967).
La Turbolenza Isotropica e' una turbolenza
con propietà statistiche che sono independenti dalla direzione.
The approach can be modified somewhat for flow in the ocean. In the idealized case of high Reynolds flow, we can calculate the statistical properties of a flow in thermodynamic equilibrium. Because the actual flow in the ocean is far from equilibrium, we assume it will evolve towards equilibrium. Holloway (1986) provides a good review of this approach, showing how it can be used to derive the influence of turbulence on mixing and heat transports. One interesting result of the work is that zonal mixing ought to be larger than meridional mixing.
Summary
Le viscosita' turbolente vorticose Ax,
Ay, e Az non possono essere
calcolate accuratamente dalla maggior parte dei flussi oceanici.
- Esse possono essere stimate dalle misure dei flussi turbolenti. Le misure nell'Oceano, sono comunque difficili; e quelle in laboratorio, sebbene accurate non possono arrivare ai numeri di Reynolds di un tipico oceano (1011).
- La teoria statistica della turbolenza fornisce utili comprensioni sul ruolo della turbolenza dell'Oceano, e questa è un area di ricerca attiva.
|
νacqua =
10-6m2/s |
|
νtar? at 15°C =
106m2/s |
|
νghiaccio =
1010m2/s |
|
Ay =
104m2/s |
8.4 La Stabilita'
Abbiamo visto nell'ultima sezione che un flusso con un numero di Reynolds abbastanza grande e' turbolento. Questa e' una forma di instabilita'. Ci sono molti altri tipi di instabilita' nell'Oceano. Ora, vedremo tre dei tipi piu' importanti:
i) la stabilita' statica associata ai cambi di densita' con la profondita',
ii) La stabilita' dinamica associata alle velocita' di shear, e
iii) La doppia-diffusione associated ai gradienti di salinita' e temperatura dell'Oceano.
Stabilita' Statica e Frequenza di Stabilita'
Consideriamo prima la stabilita' statica. Se acqua piu' densa sta' sopra acqua meno
densa, il fluido e' instabile. L'acqua piu' densa affondera' sotto l'acqua meno densa.
Al contrario, se acqua meno densa sta sopra a quella piu' densa, l'interfaccia tra
i due tipi e' stabile. Ma quanto stabile? Possiamo pensare che piu' grande il contrasto all'interfaccia We might guess that the larger the density contrast across the
interface, the more stable the interface.
Questo e' un esempio di stabilita' statica. La stabilita' statica e' importante in ogni flusso
stratificatodove la densita' aumenta con la profondita';
e quindi abbiamo bisogno di un qualche criterio per determinare l'importanza della stabilita'.
 |
| Figura 8.4 Schema per calcolare la stabilita' statica e la frequenza di stratificatione. |
Consideriamo una particella di acqua che e' spostata verticalmente ed adiabaticamente (senza scambio di calore) in un fluido stratificato (Figura 8.4). La forza di galleggiamento F che agisce sulla particella spostata e' la differenza tra il suo peso gVg ρ ' ed il peso dell'acqua intorno a lei gVg ρ2 , dove V e' il volume della particella:
|
F = gV( ρ2
- ρ' ) |
L' accelerazione della particella spostata e':
|
|
(8.20) |
ma
|
|
(8.21) |
|
|
(8.22) |
Usando la (8.21) e la (8.22) nella (8.20), ignorando i termini proporzionali a d z 2, otteniamo:
 |
(8.23) |
dove E ≡ -a / ( gdz ) e' la stabilita' della colonna d'acqua. Questo puo' essere scritto in funzione della temperatura e salinita' misurati t(z), S(z) nella colonna d'acqua (McDougall, 1987; Sverdrup, Johnson, e Fleming, 1942: 416; oppure Gill, 1982: 50):
|
|
(8.24) |
dove
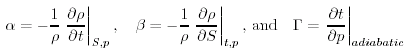 |
(8.25) |
e dove α e' il coefficiente di espansione termica,β e' il coefficiente di contrazione salina, e Γe' il (.. adiabatic lapse ..) , il cambio di temperatura con la pressione di una particella di acqua che si muove senza scambiare calore con le particelle che le sono intorno. Inoltre, p e' la pressione, t e' la temperatura in Celsius, ρ e' la densita', e S e' la salinita'.
Nei primi 1000m dell'Oceano la stabilita' e' grande, ed il primo termine della (8.23) e' molto piu' grande del secondo. Il primo termine e' proporzionale al gradiente verticale della densita' nella colonna d'acqua; il secondo termine e' proporzionale alla compressibilita' dell'acqua marina, che e' molto piccolo. Trascurando il secondo termine, possiamo scivere l'equazione della stabilita':
|
|
(8.26) |
L'approssimazione usata per ottenere la (8.26) e' valida per E > 50 × 10-8/m.
Sotto i primi 1000m dell'Oceano, il cambio di densita' con la profondita' e' cosi' piccolo che dobbiamo considerare i piccoli cambi di densita' delle particelle d'acqua, che si muovono verticalmente, dovuti alla pressione, e deve essere usata la (8.24).
La Stabilita' e' definita in tale modo
| E > 0 Stabile |
| E = 0 Neutrale |
| E < 0 Instabile |
NeI primo kilomero di Oceano, z < 1,000m, E = (50-1000)×10-8/m, e nelle fosse profonde dove z > 7,000m, E = 1×10-8/m.
L'influenza della stabilita' e' generalmente espressa da una frequenza di stabilita' N:
|
N2 ≡ -gE |
(8.27) |
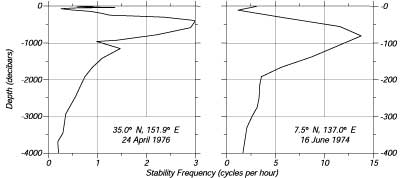
La frequenza di stabilita' e' spesso nominata: frequenza di Brunt-Vaisala oppure come frequenza di stratificazione. La frequenza quantifica l'importanza della stabilita', ed e' una variabile fondamentale nella dinamica dei flussi stratificati. In parole povere, la frequenza puo' essere interpretata come la frequenza verticale che assume una particella di fluido sottoposta ad uno spostamento verticale. Quindi, e' la frequenza massima di una onda interna dell'Oceano. Valori tipici di N sono pochi cicli per ora (Figura 8.5).
| Figura 8.6. Frequenze di stratificazione osservate nel Pacifico. A sinistra: La stabilita' del termoclino profondo ad est del 'Kuroshio'. A destra: La stabilita' del termoclino superficiale tipico dei tropici. Notare la differenza delle scale. |
La Stabilita' Dinamica ed il Numero di Richardson
Se la velocita' cambia con la profondita' in un flusso stratificato stabile, allora
il fluido puo' diventare instabile se il cambio nella velocita' con la profondita',
cioe' lo shear, e' abbastanza grande. L'esempio piu' semplice e' il vento che
soffia sopra l'Oceano. In questo caso, la stabilita' e' molto grande su tutta
la superfice marina. Possiamo dire che e' infinita perche' c'e' una discontinuita'
a scalino nella ρ (densita'), e la (8.27) diventa infinita.
Ancora, il vento che soffia su un Oceano crea le onde, e se il vento e' abbastanza forte,
la superfice diventa instabile e le onde si rompono.
Questo e' un esempio di instabilita' dinamica in cui un fluido stabile e' reso instabile dalla velocita' di 'shear'. Un'altro esempio di instabilita' dinamica, e' l'instabilita' di Kelvin-Helmholtz, che si manifesta quando il contrasto di densita' in un flusso con 'shear' e' piu' o meno come quello alla superfice del mare, come nel termoclino alla sommita' di uno strato limite stabile dell'atmosfera (Figura 8.7).
| Figura 8.7 Una nuvola ad onde mostra una instabilita' di Kelvin-Helmholtz sopra uno strato limite atmosferico stabile. Alcune onde possono diventare abbastanza alte che l'aria piu' densa sovrasta aria meno densa, e allora le onde collassano nella turbolenza. Foto con copyright Brooks Martner, NOAA Environmental Technology Laboratory. |
La relativa importanza della stabilita' statica e della instabilita' dinamica e' espressa dal Numero di Richardson:
|
|
(8.28) |
dove al numeratore troviamo lo sforzo della stabilita' statica, ed al denominatore lo sforzo della velocita' di 'shear'.
|
Ri >
0.25 |
Stabile |
|
Ri <
0.25 |
La velocita' di 'shear' aumenta la Turbulence |
Da notare che un numero di Richardson piccolo non e' il solo criterio per la instabilita'. Il numero di Reynolds deve essere grande ed il numero di Richardson deve essere inferiore a 0.25 per la turbolenza. Questi criteri sono incontrati in alcuni flussi oceanici. La turbolenza mescola il fluido in the verticale, portando ad una viscosita' vorticosa verticale ed ad una diffusivita' vorticosa. Poiche' l'Ocean tende ad essere fortemente stratificato e le correnti tendono ad essere deboli, il mescolamento turbolento e' intermittente e raro. Le misure di densita' in funzione della profondita' molto raramente mostrano fluidi piu densi sopra fluidi meno densi come si vedono nella rottura delle onde della Figura 8.7 (Moum e Caldwell 1985).
Doppia Diffusione e Dita Salate
In alcune regioni dell'Oceano, acque meno dense stanno sopra acque piu' dense,
quindi, la colonna d'acqua e' instabile sebbene non ci siano correnti.
La instabilita' accade perche' la diffusione molecolare del calore e' circa 100 volte piu'
veloce della diffusione del sale. La instabilita' fu scoperta per prima da Melvin Stern
nel 1960, che rapidamente ne capi' l'importanza in oceanografia.
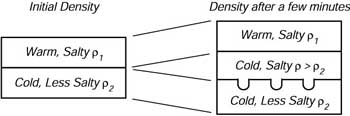
Consideriamo due strati sottili spessi pochi metri separati da una forte interfaccia (Figura 8.7). Se lo strato superiore e' caldo e salato, e se quello inferiore e' piu' freddo e meno salato di quello superiore, l'interfaccia diventa instabile anche se lo strato superiore e' meno denso di quello inferiore.
| Figura 8.8 A sinistra: distribuzione verticale iniziale della densita'. A destra: Dopo un po' di tempo, la diffusione di calore porta ad un sottile strato instabile tra i due strati inizialmente stabili. Il sottile strato instabile affonga nello strato sottostante come 'salty fingers'. La scala verticale della figura e' di pochi centimetri. |
Di seguito e' spiegato cosa succede. Il calore si diffonde attraverso l'interfaccia piu' velocemente della salinita', producendo un sottile strato freddo e salato tra i due strati iniziali. Questo strato sottile e' piu' denso di quello meno salato che sta sotto, e quindi affonda. Poiche' lo strato e' sottile, il fluido affonda in cilindri di 1-5 cm di diametro e 10cm di lunghezza, non molto differenti dalle dimensioni dei nostri diti. Questo e' chiamato diti salati (salty finges). Poiche' due costituenti si diffondono nell'interfaccia, il processo e' chiamato doppia diffusione.
Ci sono quattro variazioni in questo schema. Due variabili per due strati porta a quattro possibili combinazioni:
- Acque calde e salate sopra a quelle piu' fredde e meno salate. Questo processo e' chiamato 'dita salate' e accade nelle acque centrali di un gyre sub-tropicale, nel Nord Atlantico tropicale occidentale, e nell'Atlantico Nord-est sotto il flusso che esce dal Mare Mediterraneo. Il processo porta eventualmente ad un aumento della densita' con la profondita' in una serie di scalini. Gli strati a densita' costante sono separati da strati sottili con forti differenze in densita', ed il profilo di densita' sembra essere una scala. Schmitt et al., (1987) osservo' uno strato a scalini di 5-30m nell'Atlantico Nord tropicale occidentale, che era diffuso su 200-400km e che rimase almeno per 8 mesi. Kerr (2002) riporta che in un recente esperimento da Raymond Schmitt, James Leswell, John Toole, and Kurt Polzin mostrano 'dita salate' su acque mescolate delle Barbados 10 volte piu' veloci della turbolenza.
- Acque piu' fredde sopra quelle calde piu' salate. Questo processo e' chiamato convezione diffusiva. E' molto meno comune delle 'dita salate', e principalmente avviene ad alte latitudini. Anche la convezione diffusiva porta a scala con scalini di densita' in funzione della profondita'. Spieghiamo cosa accade in questo caso. La doppia diffusione porta ad un sottile strato caldo e meno salato alla base dello strato iniziale superiore piu' freddo e meno salato. Lo strato sottile sale e si mescola con l'acqua dello strato superiore. Un processo simile accade nello strato inferiore dove uno strato piu' freddo e salato si forma all'interfaccia. Come risultato della convezione degli strati superiori ed inferiori, l'interfaccia si rafforza; ed ogni piccolo gradiente di densita' in ogni strato e' ridotto. Neal et alt. (1969) hanno osservato strati di 2-10m di spessore nel mare sotto il ghiaccio artico.
- Acque fredde e salate sopra calde e meno salate. Sempre staticamente stabili.
- Acque calde e poco salate sopra quelle fredde e salate. Sempre stabile e la doppia diffusione dilata l'interffacia tra i due strati.
La doppia diffusione mescola le acque dell'Oceano, e non si puo' ignorare. Merryfield et alt,. (1999), usando un modello numerico della circolazione oceanica che includeva la doppia diffusione, trovarono che il mescolamento della doppia diffusione cambia la distribuzione regionale della temperatura e della salinita' sebbene ha una piccola influenza sulla circolazione a grande scala dell'Oceano.
8.5 Il Mescolamento (Mixing) nell'Oceano
L'instabilita' nell'Oceano porta al mescolamento. Poiche' l'Oceano e' stabilmente stratificato, gli spostamenti verticali devono lavorare contro la forza di galleggiamento. Il mescolamento verticale rechiede piu' energia di quello orizzontale. Piu' grande e' la frequenza di stabilita': piu' grande sara' il lavoro richiesto per il mescolamento verticale. Di conseguenza, il mescolamento orizzontale lungo le superfici a densita' costante e' molto piu' grande di quello verticale attraverso le superfici a densita' costante. L'ultimo, comunque, generalmente chiamato 'diapycnal mixing', e' molto importante perche' cambia la struttura verticale dell'Oceano, e controlla in gran parte (.. the rate at which deep water eventually reaches the surface in mid and low latitudes. ..)
L'equazione per il mescolamento verticale da vortici di un tracciante Θ come la salinita' o la temperatura è:
|
|
(8.29) |
dove Kz e' la diffusivita' verticale vorticosa, W e' la velocita' verticale media, e S e' il termine della sorgente.
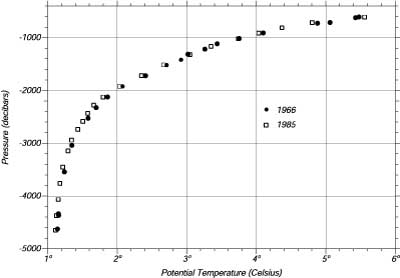
| Figura 8.8 Temperatura Potenziale misurata in funzione della profondita' (pressione) vicino 24.7°N, 161.4°W nel Pacifico Centrale Nord dalla R/V Yaquina nel 1966 (•), e dalla R/V Thompson in 1985 (°). I dati provengono dagli Atlanti delle sezioni degli Oceani prodotte da Swift, Rhines, and Schlitzer. |
Mescolamento Verticale Medio
Walter Munk (1966) uso' un'osservazione molto semplice per calcolare il mescolamento
verticale nell'Oceano. Egli osservo' che l'Oceano ha un termoclino quasi ovunque,
ela parte piu' profonda del termoclino non cambia anche per decadi (Figure 8.8).
Questa fu' una osservazione molto importante perche' ci aspettiamo che il mescolamento
verso il basso dovrebbe continuamente approfondire il termoclino. Ma non e' cosi'.
Quindi, un termoclino stazionario richiede che il mescolamento verso il basso del
calore deve essere bilanciato da un trasporto verso l'alto del calore da una corrente
verticale media W. Questo e' il risultato della (8.29) per uno stato stazionario
dove non ci sono ne sorgenti ne buchi:
|
|
(8.30) |
dove T e' la temperatura in funzione della profondita' del termoclino.
L'equazione ha come soluzione:
|
T » T0
exp (z / H) |
(8.31) |
dove H = Kz /W e' la (.. scale depth ..) del termoclino, e T0 e' la temperatura vicino la cima del termoclino. Le Osservazioni della forma del termoclino profondo sono molto vicine a quella di una funzione esponenziale. Munk uso' una funzione esponenziale per (.. function fit through ..) le osservazioni di T(z) per ottenere H.
Munk calcolo' W dalle distribuzioni verticali osservate di 14C, un isotopo radiattivo del carbonio, per ottenere una scala temporale verticale. In Questo caso, S = -1.24 × 10-4 anni-1. Le scale del tempo e dello spazio danno W = 1.2 cm/giorno e
|
< Kz
> = 1.3 × 10-4m2/s |
Diffusivita' vorticosa verticale media |
(8.32) |
dove le parentesi denotano la media della diffusivita' vorticosa del termoclino.
Munk uso' ancora la W per calcolare la media del flusso verticale attraverso il termoclino nel Pacifico, ed il flusso era in buon accordo con il tasso di formazione dell'acqua profonda assumendo che questa sale quasi dovunque allo stesso valore nel Pacifico. Globalmente, la sua teoria richiede una risalita di 25-30 Sv, dove uno Sverdrup e' il flusso di 106 metri cubi al secondo.
Le osservazioni di Munk hanno un'altra importante conseguenza. Poiche' il termoclino esiste quasi dovunque, ci deve essere una corrente verso l'alto quasi dovunque. Torneremo su questo quando analizzeremo la teoria di Stommel per la circulazione profonda nel §13.2.
La Misura del Mescolamento Verticale
Le osservazioni dirette del mescolamento verticale richiedono lo sviluppo di tecniche
appropiate:
i) La struttura fine della turbolenza, comporta sonde capaci di misurare temperatura e salinita con una risoluzione spaziale di pochi centimetri (Gregg 1991), e
ii)la distribuzione di traccianti come lo zolfo esafluoride (SF6) che puo' essere facilmente riconosciuto a concentrazioni molto basse come un grammo in un kilometro cubo di acqua marina.
Misure dirette in Oceano aperto di turbolenza e di diffusione di SF6 portano ad una diffusività vorticosa:
|
Kz ≈ 10-5m2/s |
Diffusivita' Vorticosa Verticale di Oceano Aperto |
(8.33) |
Per esmpio, Ledwell, Watson, e Law (1991) iniettarono 139kg di SF6 nell'Atlantico vicino a 26°N, 29°W, 1200 km ad ovest delle isole Canarie ad una profondita' di 310m. Poi misurarono la concentrazione per cinque mesi su come il mescolamento avveniva su centinaia di chilometri ed ottennere una diffusivita' 'diapycnal' vorticosa di Kz = 1.1 ± 0.2 × 10-5 m2/s.
Questi ed altri esperimenti di Oceano aperto indicano che il mescolamento turbolento è guidato dalla rotture delle onde interne e dalla instabilita' dello 'shear' ai confini. Comunque, il mescolamento per turbolenza sembra essere piu' importante della doppia diffusione (Gregg 1987).
La grande discrepanza tra i calcoli di Munk sulla diffusivita' media vorticosa per mescolamento verticale ed i valori osservati nell'Oceano aperto suggeriscono ulteriori esperimenti per risolvere la differenza. Due recenti esperimenti sono particolarmente interessanti perche' indicano che sopra ai monti ed alle dorsali sottomarine
|
Kz ≈ 10-3 m2/s |
Diffusivita' Vorticosa Verticale da Fondo 'Rough' frastagliato? |
(8.34) |
Polzin et al., (1997) hanno misurato la struttura verticale della temperatura nel Bacino Brasiliano dell'Atlantico Meridionale. Hanno trovato Kz > 10-3m2/s vicino al fondo quando l'acqua fluisce sul fianco occidentale della dorsale Atlantica e sul bordo orientale del bacino. Kunze e Toole (1997) calcolo enhanced eddy diffusivity as large as K = 10-3 m2/s sopra il Fieberling Guyot nel Pacifico di Nord-ovest ed una piccola diffusivita' lungo i fianchi del monte sottomarino.
I risultati di questo ed altri esperimenti mostrano che il mescolamento avviene principalmente dalla rottura delle onde interne dallo 'shear' ai bordi degli oceani: lungo le pendici continentali, sopra i monti sottomarini e sulle dorsali medio-oceaniche, nei fronti, e nello strato mescolato alla superfice marina. In gran parte, il mescolamento e' forzato dalle correnti di marea di Oceano profondo, che diventa turbolento quando il flusso passa gli ostacoli sul fondo marino, includendo i monti e le dorsali medio-oceaniche (Jayne et al, 2004).
Ancora, il mescolamento osservato in Oceano aperto lontano dai bordi e' troppo piccolo per stimare il mescolamento calcolato da Munk. Un recente lavoro presentato alla Conferenza del 'World Ocean Circulation Experiment' sulla Circolazione e Clima (1998), il lavoro di Munk e Wunsch (1998) e quello di Webb e Suginohara (2001) indicano che il dilemma puo' essere risolto in piu modi:
- Primo, gli studi separati di Gargett, Salmon, e Marotzke mostrano che dobbiamo separare il concetto di convezione profonda da quello della controcorrente lungo i meridiani (vedi il capitolo 13). La convezione profonda puo' mescolare propieta' ma non la massa. La massa di acqua di risalita richiesta da Munk puo' essere sovrastimata, ed il mescolamento verticale necessario a bilanciare la risalita può essere più piccolo di quello da Lui calcolato. Webb e Suginohara (2001) notano che l'acqua di risalita potrebbe essere solo 8Sv.
- Secondo, il mescolamento probabilmente ha luogo lungo i confini nelle regioni di produzione per le acque di termoclino (Gnadadesikan, 1999). Ad esempio, le acque a 1200m nell'Atlantico centrale del Nord si potrebbero muovere orizontalmente verso la 'Gulf Stream', dove si mescola con acque da 1000m. L'acqua risultante si potrebbe muovere orizzontalmente indietro nell'Atlantico centrale del Nord ad una profondita' di 1100m. In tal modo, acque a 1200m ed a 1100m possono raggiungere la loro posizione lungo percorsi interamente differenti.
Measured Horizontal Mixing
Eddies mix
fluid in the horizontal, and large eddies mix more fluid than small
eddies. Eddies range in size from a few meters due to turbulence in the
thermocline up to several hundred kilometers for geostrophic eddies
discussed in Chapter 10.
In general, mixing depends on Reynolds number R (Tennekes 1990: p.11)
|
|
(8.35) |
where γ is the molecular diffusivity of heat. Furthermore, horizontal eddy diffusivity is ten thousand to ten million times larger than the average vertical eddy diffusivity.
L'equazione (8.35) implica Kx ≈ UL. Questa forma funzionale e' in buon accordo con l'analisi di Joseph e Sender's (1958), come riportato da (Bowden 1962), sulla dispersione dei traccianti radioattivi, della torbidita' ottica, delle acque Mediterranee nel Nord Atlantico. Essi riportano
|
Kx =
PL |
(8.36) |
|
10 km < L < 1500 km |
|
|
P = 0.01 ± 0.005
m/s |
dove L e' la distanza dalla sorgente, e U e' constante.
La diffusivita' vorticosa orizzontale (8.35) è in buon accordo anche con recenti lavori sulla diffusivita' orizzontale. Il lavoro di Holloway (1986) che ha usato osservazioni dai satelliti altimetrici delle correnti geostrofiche, Freeland et al., (1975) che hanno tracciato boe alla deriva sommerse SOFAR, McWilliams (1976) e Ledwell et al., (1998) che usano osservazioni di correnti e traccianti per trovare
|
Kx ≈ 8×102
m2/s |
Diffusivita' Geostrofica Vorticosa Orizzontale |
(8.37) |
Usando la (8.36) e il misurato Kx, implica vortici con scale tipiche di 80 km, un valore vicino la misura dei vortici geostrofici responsabili del mescolamento.
Anche Ledwell, Watson, e Law (1991) hanno misurato la diffusivita' orizzontale vorticosa. Loro trovano
|
Kx ≈ 1 - 3 m2/s |
Open-Ocean Horizontal Eddy Diffusivity |
(8.38) |
su scale di pochi metri dovuto alla turbolenza nel termoclino probabilmente forzato dalla rottura delle onde interne. Questo valore, quando è usato nella (8.36) implica lunghezze tipiche di 100 m per piccoli vortici responsabili del mescolamento in questo esperimento.
Commenti sul mescolamento orizzontale
- L'Acqua all'interno dell'Oceano sembra muoversi lungo le superfici a densita'
constante con un piccolo mescolamento locale fino a quando raggiungono un
confine dove sono mescolate verticalmente. Le acque mescolate allora si muovono
di nuovo verso l'Oceano aperto lungo superfici a densita' costante (Gregg
1985).
Un caso particolare e' interessante osservare. Quando l'acqua mescolata verso il basso attraverso la base dello strato limite fluisce fuori del termoclino lungo superfici a densita' costante, il mescolamento porta al modello di termoclino ventilato della distribuzioni di densita' oceaniche. - Le osservazioni del mescolamento dell'Oceano implicano che i modelli numerici della circolazione Oceanica dovrebbero usare schemi di mescolamento che hanno una diffusivita' vorticosa parallela e perpendicolare alle superfici con densita' costante, invece delle superfici a z costante come sopra. Il mescolamento orizzontale lungo superfici a z costante porta al mescolamento tra gli strati a densita' costante perche' gli strati a densita' costante sono inclinati rispetto a quelli orizzontali di circa 10-3 radianti (vedi §10.7 e la Figura 10.13). Gli studi di Danabasoglu, McWilliams, e Gent (1994) mostra che i modelli numerici che usano mescolamenti (.. isopycnal and diapycnal ..) portano ad una simulazione molto piu' realistica della circolazione Oceanica.
8.6 Concetti Importanti
- L'attrito nell'Oceano e' importante solo su distanze di pochi millimetri.
Per la maggior parte dei flussi, l'attrito puo' essere ignorato.
- L'Oceano e' turbolento per tutti i flussi delle dimensioni tipiche che
oltrepassano pochi centimetri, la teoria per i flussi turbolenti nell'Oceano
non e' ancora ben compresa.
- L'influenza della turbolenza e' in funzione del numero di Reynolds del
flusso. I flussi con la stessa geometria e lo stesso numero di Reynolds hanno
le stesse linee di corrente.
- Gli oceanografi assumono che la turbolenza influisce sui flussi con
distanze tipiche piu' grandi di pochi centimetri nello stesso modo in cui la viscosita'
molecolare influisce sui flussi con distanze molto piu' piccole.
- L'influenza della turbolenza porta ai termini degli sforzi di Reynolds
nell'equazione del momento.
- L'influence della stabilita' statica nell'Oceano e' espressa come una
frequenza, la frequenza di stabilita'. Piu' grande e' la frequenza, piu' stabile
e' la colonna d'acqua.
- L'influence della stabilita' della deformazione (shear stability) e' espressa
con il numero di Richardson. Piu' grande la velocita' (shear), e piu' debole la
stabilita' statica, e piu' verosimilmente il flusso diventera' turbolento.
- La diffusione molecolare del calore e' molto piu' veloce della diffusione
della salinita'. Questo induce alla instabilita' della doppia diffusione che modifica
la distribuzione nella colonna d'acqua in molte regioni dell'Oceano.
- L'instabilita' nell'Oceano porta al mescolamento (mixing). Il mescolamento
perpendicolare alle superfici di densita' costante e' molto piu' piccolo di quello lungo
queste superfici.
- La diffusivita' vorticosa orizzontale nell'Oceano e' molto piu' grande di quella
verticale.
- Le misure della diffusivita' vorticosa indicano che l'acqua e' mescolata verticalmente vicino ai confini dell'oceano come sopra ai monti sottomarini e sopra alle dorsali medio-oceaniche.
Robert H. Stewart, stewart@ocean.tamu.edu
All contents copyright © 2005 Robert H. Stewart,
All rights reserved
Updated on Marzo 16, 2008