Capitolo 9 - La Risposta dell'Oceano Superficiale al Vento

Se avete avuto modo di viaggiare per gli Stati Uniti, avrete notato che il clima della costa orientale differisce considerevolmente da quello della costa occidentale. Perché? Perché il clima di Charleston, Sud Carolina è così differente da quello di San Diego, sebbene sono entrambi a circa 32° N, ed entrambi sono sull'oceano? Charleston riceve 25-150 cm di pioggia all'anno, San Diego solo 25-50 cm; Charleston ha estati calde, San Diego ha estati fredde. Oppure perché il clima di San Francisco è così differente da quello di Norfolk, Virginia?

Se guardiamo da vicino alle caratteristiche dell'atmosfera lungo le due coste intorno al 32°N, troviamo altre differenze che possono spiegare il clima. Per esempio, quando il vento soffia dal mare verso San Diego, porta un ' boudary layer' di poche centinaia di metri con aria fredda, umida e marina con sopra aria calda e secca. Sulla costa orientale, quando il vento soffia verso terra, porta un strato limite caldo, umido e marino che è molto più alto. La convezione, che produce pioggia, è molto più frequente sulla costa orientale, che su quella occidentale. Allora perché lo strato limite atmosferico sopra il mare è cosi diverso sulle due coste? La risposta può in parte essere trovata studiando la risposta dell'oceano ai venti locali, il soggetto di questo capitolo.

9.1 Il Moto Inerziale

Per cominciare il nostro studio delle correnti vicino la superfice, consideriamo prima una soluzione molto semplice delle equazioni del moto, la risposta dell'oceano ad un impulso che mette in moto l'acqua. Per esempio, l'impulso può essere un vento forte che soffia per poche ore. L'acqua allora si muove sotto l'influenza della forza di Coriolis e della gravità. Nessuna altra forza agisce sull'acqua.

Tale moto è detto inerziale. La massa dell'acqua continua a muoversi solo per la sua inerzia. Se l'acqua fosse nello spazio, si dovrebbe muovere in una linea retta, in accordo alla seconda legge di Newton. Ma nella Terra, che ruota, il moto è molto differente.

Dalla (7.12) Le equazioni del moto per un oceano senza attrito diventano:

	(9.1a)
	(9.1b)
	(9.1c)

dove p è la pressione, Ω = 2 π/(giorno siderale ) = 7.292 × 10^-5 rad/s è la rotazione della Terra in coordinate fisse, e φ è la latitudine. Noi abbiamo anche usato F_i = 0 perché il fluido è senza attrito.

Ora cerchiamo una semplice soluzione a queste equazioni. Per farlo dobbiamo semplificare le equazioni del momento. Primo, se solo la gravità e la forza di Coriolis agiscono sull'acqua, non ci devono essere gradienti orizzontali di pressione:

Inoltre, possiamo assumere che il flusso sia orizzontale, e la (9.1) diventa:

	(9.2a)
	(9.2b)

dove:

(9.3)

è il Parametro di Coriolis e Ω = 7.292 × 10^-5rad/s è la velocità angolare della Terra.

Le equazioni (9.2) sono due equazioni accoppiate, di primo ordine, lineari, differenziali, che possono essere risolte con tecniche standard. Se risolviamo la seconda equazione per u, e la inseriamo nella prima equazione otteniamo:

Riarrangiando l'equazione la mettiamo in una forma standard da cui dovremmo riconoscere, l'equazione di un oscillatore armonico:

(9.4)

che ha la soluzione (9.5). Questa corrente è detta corrente inerziale oppure oscillazione inerziale:

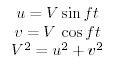(9.5)

Notare che le (9.5) sono le equazioni parametriche per un cerchio con diametro D_i = 2V/f e periodo T_i = (2π)/f = T_sd /(2 sin φ) dove T_sd è il giorno siderale.

T_i è il periodo inerziale, ed è la metà del tempo richiesto per la rotazione di un piano locale sulla superfice terrestre (Tabella 9.1). La direzione di rotazione è anti-ciclonico: orario nell'emisfero nord, antiorario in quello sud. Le correnti inerziali sono il moto libero delle particelle di acqua in un piano rotante.

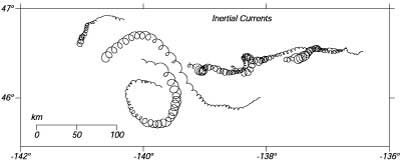
Le correnti inerziali sono le più comuni correnti del mare (Figura 9.1). Webster (1968) ha rivisitato molti rapporti pubblicati sulle correnti inerziale ed ha trovato queste correnti sono state osservate a tutte le profondità ed a tutte le latitudini. I moti sono transitori e decadono in pochi giorni. Le oscillazioni a differenti profondità oppure a differenti siti vicini sono generalmente incoerenti.

Figura 9.1 Correnti Inerziali del Pacifico Nord in Ottobre (giorni 275-300) misurate da buoy 'holey-sock' alla deriva ad una profondità di 15m. Le posizioni sono state osservate 10-12 volte al giorno dal sistema Argos sul satellite metereologico polare del NOAA satellite ed interpolate a posizioni ogni tre ore. Le correnti più grandi sono state generate da una tempesta il giorno 27/7. Notare che non sono vortici individuali. L'intera superfice sta ruotando. Una boa posizionata in qualunque parte della regione ha lo stesso movimento circolare. Da Van Meurs (1998).

Le correnti inerziali sono causate da cambiamenti rapidi del vento sulla superfice del mare, con i rapidi cambiamenti dei venti forti che producono le oscillazioni più grandi. Sebbene abbiamo derivato le equazioni per le oscillazioni assumendo un flusso senza attrito, l'attrito non può essere completamente ignorato. Con il tempo, le oscillazioni decadono in altre correnti di superfice. (vedi, per esempio, Apel, 1987: -6.3 per maggiori informazioni.)

9.2 Lo Strato di Ekman alla superfice del Mare

I venti costanti che soffiano sulla superfice marina producono uno strato limite sottile, orizzontale lo strato di Ekman. Per sottile, intendo uno strato che è al massimo spesso poche centinaia di metri. che è sottile comparato alla profondità dell'acqua di un oceano. Uno strato simile esiste anche al fondo del mare, lo Strato di Ekman del fondo, e nella bassa atmosfera proprio sopra la superfice marina, lo strato limite planetario (lo strato di attrito) descritto nel §4.3. Lo strato è detto di Ekman dopo che il Professor Walfrid Ekman, ne ha compreso la dinamica con la sua tesi di dottorato.

Il lavoro di Ekman fu il primo di una serie di studi straordinari condotti nella prima metà del novecento, che hanno portato alla comprensione di come i venti forzano la circolazione oceanica (Tabella 9.2). In questo capitolo consideriamo i lavori di Nansen e di Ekman. Il resto della storia è dato nel capitolo 11 e 13.

Argomenti Qualitativi di Nansen
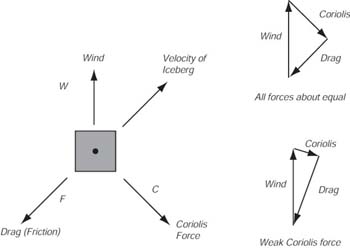
Fridtjof Nansen notò che, nel mare Artico guardando da sottovento, il vento tendeva a muovere il ghiaccio con un angolo di 20°-40° alla destra del vento (vedi Figura 9.2). Più tardi lavorò sul bilancio delle forze, che devono esistere quando il vento prova a spingere gli iceberg in una Terra rotante.

Figura 9.2 Il bilancio delle forze, che agiscono su un iceberg, sulla Terra rotante, quando soffia il vento.

Nansen dimostrò che tre forze dovevano essere importanti:

1. Lo sforzo del vento, W;
2. l'attrito F (altrimenti l'iceberg si sarebbe mosso alla stessa velocità del vento);
3. La forza di Coriolis, C.

Nansen dimostro altresì che le forze dovevano avere i seguenti attributi:

1. L'attrito doveva essere opposto alla direzione della velocità del ghiaccio;
2. La forza di Coriolis deve essere perpendicolare alla velocità;
3. Le forze devono bilanciarsi per un flusso stazionario.

La Soluzione di Ekman
Nansen chiese a Vilhelm Bjerknes di far fare ad uno dei suoi studenti lo studio teorico dell'influenza della rotazione terrestre sulle correnti forzate dal vento. Walfrid Ekman fu scelto, e lui presento i risultati nella sua tesi a Uppsala. Ekman più tardi espanse lo studio per includere l'influenza dei continenti e le differenze di densità dell'acqua (Ekman, 1905). Nel seguito è riportato la linea di ragionamento del lavoro.

Ekman assume un flusso stazionario, omomogeneo, orizzontale, con attrito, su una Terra ruotante. Dunque le derivate orizzontali e temporali sono zero:

(9.6)

Ekman assume inoltre una viscosità costante per i vortici verticali (8.12):

(9.7)

dove T_xz, T_yz sono le componenti dello sforzo del vento nella direzione x, y , e ρ_w è la densità dell'acqua di mare.

Con queste assunzioni, e usando la (9.7) nella (8.14), le componenti x e y del l'equazione del momento hanno la semplice forma:

	(9.8a)
	(9.8b)

dove f è il parametro di Coriolis; é facile verificare che le equazioni (9.8) hanno le soluzioni:

	(9.9a)
	(9.9b)

quando il vento sta soffiando verso nord (T = T_yz ). Le constanti sono

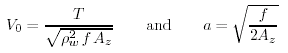(9.10)

e V₀ é la velocità della corrente alla superfice del mare.

Guardiamo ora alla forma delle soluzioni. Alla superfice del mare z = 0, exp(z = 0) = 1, e

	(9.11a)
	(9.11b)

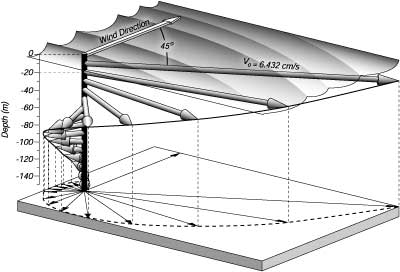
La corrente ha una velocità di V₀ verso nord-est. In generale, la corrente di superfice è a 45° a destra del vento, guardando da sottovento nell'emisfero settentrionale. La corrente è a 45° alla sinistra del vento nell'emisfero meridionale. Sotto la superfice, la velocità decade esponenzialmente con la profondità (Figure 9.3):

(9.12)

Figura 9.3. Corrente di Ekman generata da un vento da 10m/s a 35°N.

I Valori delle Costanti di Ekman
Per procedere ulteriormente, abbiamo bisogno dei valori per ognuno dei parametri liberi: la velocità alla superfice, V₀; il coefficiente di viscosità turbolenta, A_z; o lo sforzo del vento T.

Lo sforzo del vento è ben conosciuto, ed Ekman usò la bulk formula (4.2):

(9.13)

dove ρ_air è la densità dell'aria, C_D è il coefficiente di attrito, e U₁₀ è la velocità del vento a 10m sopra il livello del mare. Ekman prese dalla bibliografia i valori per la V₀ in funzione della velocità del vento. Trovò:

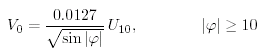(9.14)

Con questa informazione, quindi, poteva calcolare la velocità in funzione della profondità, conoscendo la velocità U₁₀ e la direzione del vento.

La Profondità dello Strato di Ekman
Lo spessore dello strato di Ekman è arbitrario perché le correnti di Ekman decrescono esponenzialmente con la profondità. Ekman propose che lo spessore fosse la profondità D_E a cui la velocità della corrente è opposta alla velocità della superfice, che si trova ad una profondità D_E = π/a, e la profondità dello strato di Ekman è:

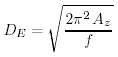(9.15)

Usando la (9.13) nella (9.10) , dividendo per U₁₀, ed usando la (9.14) e la (9.15) abbiamo:

(9.16)

in unità SI; il vento in metri al secondo dà la profondità in metri. La constante nella (9.16) è basata su ρ_w = 1027 kg/m³, ρ_air = 1.25 kg/m³, ed il valore di Ekman' della C_D = 2.6×10^-3 per il coefficiente di attrito.

Usando la (9.16) con venti tipici, la profondità dello strato di Ekman varia da circa 45m a 300m (Tabella 9.3), e la velocità della corrente superficiale varia da 2.5% al 1.1% della velocità del vento dipendendo dalla latitudine.

Il Numero di Ekman: Le Forze di Coriolis e dell'Attrito La profondità dello strato di Ekman è strettamente legato alla profondità alla quale la forza di attrito è uguale alla forza di Coriolis nell'equazione del momento (9.9) . La Forza di Coriolis è fu, e la forza di attrito è A_z ∂²U/∂z². Il rapporto delle forze, che è non dimensionale, è detto Numero di Ekman E_z:

(9.17)

dove abbiamo approssimato i termini usando velocità tipiche u, e profondità tipica d. Il subscritto z è necessario perché l'Oceano stratificato e mescolato nella verticale è molto meno mescolato in orizzontale. Da notare, che come la profondità aumenta, l'attrito diventa piccolo ed eventualmente rimane soltanto la forza di Coriolis.

Risolvendo la (9.17) per d abbiamo

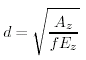(9.18)

che è in accordo con la forma funzionale della (9.15) proposta da Ekman. Eguagliando la (9.18) e la (9.15) richiede che E_z = 1/(2π²) = 0.05 alla profondità di Ekman. Così Ekman sceglie una profondità alla quale le forze di attrito sono molto più piccole di quella di Coriolis.

Lo Strato di Ekman di Fondo
Lo strato di Ekman al fondo e nell'atmosfera differiscono dallo strato alla superfice del mare. La soluzione per lo strato di fondo sotto ad un fluido con velocità U nella direzione x è:

La velocità và a zero al limite, u = v = 0 a z = 0. La direzione del flusso vicino al limite è 45° a sinistra del flusso U fuori dello strato limite nell'emisfero nord; e la direzione del flusso ruota con la distanza sopra il limite (Figura 9.4). La direzione di rotazione è anti-ciclonica con la distanza dal fondo.

Figura 9.4 Strato di Ekman per il kilometro più basso nell'atmosfera (linea solida), insieme con le velocità del vento misurate da Dobson (1914). Il numero dà l'altezza in metri dalla superfice. Lo strato limite al fondo dell'oceano ha una forma simile. Da Houghton (1977).

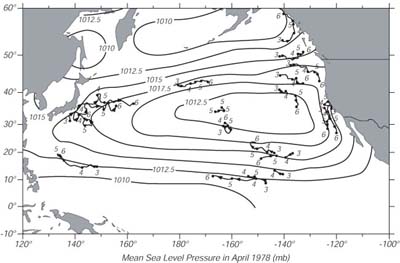
I venti sopre lo strato limite planetario sono perpendicolari al gradiente di pressione nell'atmosfera e paralleli alle linee di pressione superficiale costante. I venti alla superfice sono a 45° alla sinistra dei venti sopra di loro, e le correnti di superfice sono a 45° alla destra del vento alla superfice. Quindi ci aspettiamo che le correnti alla superfice del mare siano quasi nella direzione dei venti sopra lo strato limite planetario e paralleli alle linee di pressione costante. Le osservazioni dei drifter superficiali nel Pacifico tendono a confermare le ipotesi (Figura 9.5).

Figura 9.5 Traiettorie dei drifter di superfice nell'Aprile del 1978 insieme con la pressione atmosferica alla superfice, mediata su un mese. Notare che i drifter tendono a seguire le linee di pressione costante eccetto nel Kuroshio dove le currenti marine sono più veloci comparate alle velocità nello strato di Ekman nell'Oceano. Da McNally, et al. (1983).

Esaminando le Assunzioni di Ekman
Prima di considerare la validità della teoria di Ekman per descrivere il flusso nello strato limite della superfice dell'Oceano, esaminiamo , prima, la validità delle assunzioni di Ekman. Lui assume:

1. Nessun confine. Questo è valido lontano dalle coste.
2. Acqua profonda. Questo è valido se la profondità >> 200m.
3. f-plane. Questo è valido.
4. Stato stazionario. Questo è valido se il vento soffia per più di un 'pendulum day'. Notare comunque che anche Ekman calcola una soluzione dipendente dal tempo, come fece Hasselmann (1970).
5. A_z è una funzione di U ²₁₀ soltanto; é assunta essere independente dalla profondità. Questa non è una buona assunzione. Il mixed layer può essere più sottile della profondità di Ekman, e A_z cambierà rapidamente al fondo dello strato mescolato perché il mescolamento è una funzione della stabilità. Il mescolamento attraverso uno strato stabile è molto minore che attraverso uno strato a stabilità neutra. Profili più realistici, per il coefficiente di viscosità turbolenta in funzione della profondita cambiano la forma dei profili di velocità calcolati. Riconsidereremo questo problema di seguito.
6. densità omogenea. Questo è probabilmente buono, eccetto per i suoi effetti sulla stabilità.

Osservazioni del Flusso Vicino la Superfice del Mare
Il Flusso alla superfice del mare è in accordo con la teoria di Ekman? Le misure di corrente fatte durante molti esperimenti molto accurati indicano che la teoria di Ekman è notevolmente buona. La teoria descrive accuratamente il flusso mediato su molti giorni. Le misure mettono anche in evidenza le limitazioni della teoria.

Weller e Plueddmann (1996) misurarono correnti da 2 m a 132 m usando 14 correntometri a media vettoriale posizionati dalla Piattaforma Strumentale Gallegiante FLIP nel Febbraio e Marzo 1990 500 km ad ovest di Capo Conception, California. Questo fu l'ultimo di una serie notevole di esperimenti coordinata da Weller, usando strumenti sul FLIP.

Davis, DeSzoeke, e Niiler (1981) misurarono correnti da 2m a 175m usando 19 correntometri a media vettoriale posti in un ancoraggio per 19 giorni nell'Agosto e Settembre 1977 a 50°N, 145°W nel nord-est del Pacifico.

Ralph and Niiler (2000) tracciarono 1503 drifter a 15m depth nel Pacifico dal Marzo 1987 a Dicembre 1994. La velocità del vento fu ottenuta ogni 6 ore dall' European Centre for Medium-Range Weather Forecasts ECMWF.

I risultati dell'esperimento indicano che:

1. Le correnti inerziali sono la componente più grande del flusso.
2. Il flusso è quasi indipendente dalla profondità dello strato mescolato per periodi vicini a quello inerziale. Così lo strato mescolato si muove come una piastra al periodo inerziale. La corrente è concentrata alla cima del termoclino.
3. Il flusso mediato su molti periodi inerziali è quasi esattamente quello calcolato dalla teoria di Ekman. Il profilo (lo 'shear') delle correnti di Ekman si estende attraverso il mixed layer mediato e dentro il termoclino. Ralph e Niiler trovano:

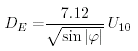   	(9.20)
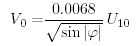   	(9.21)

   La profondità dello strato di Ekman D_E è quasi esattamente quella proposta da Ekman (9.16), ma la corrente di superfice V₀ è la metà del suo valore (9.14).

4. Il trasporto è a 90° alla destra del vento nell'emisfero settentrionale. La direzione del trasporto è in buon accordo con la teoria di Ekman.

Influenza della Stabilità nello Strato di Ekman
Ralph e Niiler (1999) fanno notare che la scelta di Ekman di una equazione per le correnti superficiali (9.14), che porta alla (9.16), è consistente con le teorie che includono l'influenza della stabilità nella parte alta dell'Oceano. Le correnti con periodi vicini a quello inerziale produce (shear) nel termoclino. Lo shear mescola gli strati superficiali quando il numero di Richardson cade sotto il valore critico (Pollard et al., 1973). Questa idea, quando è inclusa nelle teorie del mixed-layer , porta a una corrente di superfice V₀ che è proporzionale a O(N/f)

(9.22)

ed inoltre

(9.23)

Notare che la (9.22) e la (9.23) sono ora dimensionalmente corrette. Le equazioni usate prima, (9.14), (9.16), (9.20), e (9.21) rechiedono tutte un coefficiente dimensionale.

9.3 I Trasporti di Massa di Ekman

Il flusso dello strato di Ekman alla superfice del mare trasporta massa. Per molte ragioni vogliamo conoscere la massa totale trasportata nello strato. Il trasporto di massa di Ekman M_E è definito come l'integrale della velocità di Ekman U_E, V_E dalla superfice alla profondità sotto lo strato di Ekman. Le due componenti del trasporto sono M_Ex, M_Ey:

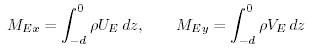(9.24)

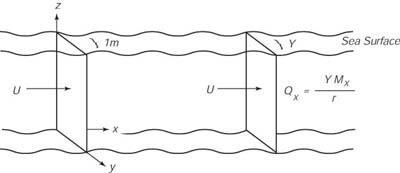
Il trasporto ha le unità kg/(m · s); ed è la massa di acqua che passa attraverso un piano verticale largo un metro che è perpendicolare al trasporto che si stende dalla superfice alla profondità -d (Figura 9.6).

Figura 9.6 Disegno per definire A sinistra: il trasporto di massa, e A destra: il trasporto del volume.

Calcoliamo i trasporti di massa di Ekman integrando la (8.14) nella (9.24):

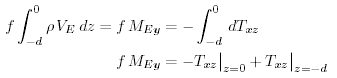(9.25)

Poche centinaia di metri sotto la superfice le velocità di Ekman si avvicinano allo zero, e l'ultimo termine della (9.25) è zero. Così il trasporto è dovuto solo allo sforzo del vento alla superfice del mare. (z = 0). In modo simile, possiamo calcolare il trasporto nella direzione x per ottenere le due componenti del trasporto di massa di Ekman:

	(9.26a)
	(9.26b)

dove T_xz(0) , T_yz(0) sono le due componenti dello sforzo alla superfice marina. Notiamo che il trasporto è perpendicolare allo sforzo del vento, ed alla sinistra del vento nell'emisfero settentrionale. Se il vento verso nord è nella direzione positiva y (un vento da sud), allora T_xz(0) = 0, M_Ey = 0; e M_Ex = T_yz(0)/ f. Nell'emisfero settentrionale, f è positivo, ed il trasporto di massa è nella direzione x, verso est.

Può sembrare strano che il trascinamento del vento sull'acqua porta a correnti perpendicolari alla direzione del trascinamento. Il risultato viene dall'assunzione che l'attrito è confinato in un sottile strato limite superficiale che è zero all'interno dell'oceano, e che la corrente è in equilibrio con il vento così che non è più accellerato.

Il trasporto del volume Q è il trasporto di massa diviso per la densità dell'acqua e moltiplicato per la larghezza perpendicolare al trasporto.

(9.27)

dove Y è la distanza nord-sud attraverso la quale il trasporto verso est Q_x è calcolato, e X è la distanza est-ovest attraverso il trasporto verso nord Q_y è calcolato. Il trasporto del volume come dimensioni i metri cubi per secondo. Una unità conveniente per il trasporto di volume nell'oceano è il milione di metri cubi al secondo. Questa unità è chiamata Sverdrup, ed è abbreviata con Sv.

Osservazioni recenti del trasporto di Ekman nell'oceano coincide con i valori teorici della (9.26). Chereskin e Roemmich (1991) misurano il trasporto del volume di Ekman al 11°N nell'Atlantico usando un profilatore acustico di corrente ad effetto Doppler descritto nel capitolo 10. Loro calcularono un trasporto verso sud Q_y = 12.0 ± 5.5Sv dalle misure dirette di corrente, Q_y = 8.8 ± 1.9Sv dal vento misurato usando la (9.26) e la (9.27), e Q_y = 13.5 ± 0.3Sv dai venti medi mediati su molti anni al 11°N.

L'Uso dei Trasporti
I trasporti sono molto usati per due importanti ragioni. Primo, il calcolo è molto più efficace di quelli delle velocità nello strato di Ekman. Per efficaca, intendo che i l calcolo è basato su minori assunzioni, e che i risultati sembrano più corretti. In tal modo, il trasporto di massa calcolato non dipende dal conoscere la distribuzione della velocità nello strato di Ekman o dalla viscosità dei vortici.

Secondo, la variabilità del trasporto spaziale ha importanti conseguenze. Vediamo le applicazioni nel seguito.

9.4 Applicazione della Teoria di Ekman

Poiché i venti che soffiano sul mare, producono uno strato di Ekman, che trasporta acqua ad angolo retto rispetto alla direzione del vento, ogni variabilità spaziale del vento, oppure i venti che soffiano lungo alcune coste, possono portare ad 'upwelling'. E l'upwelling' è importante: è una risalita alla superfice di acque profonde.

1. L'upwelling aumenta la produttività biologica, che ricordiamo nutre i pesci.
2. L' acqua fredda, che risale, altera il tempo locale. L'aria che va sulla terraferma da regioni di upwelling, tende a portare nebbia, nuvole basse, una stabile atmosfera stratificata, poca convezione e poca pioggia.
3. La variabilità spaziale del trasporto in mare aperto porta all' upwelling ed al suo contrario downwelling, che ridistribuiscono la massa nell'Oceano, e che porta alle correnti geostrofiche guidate dal vento attraverso la 'Ekman pumping': un processo che vedremo nel caitolo 11.

Upwelling costiero
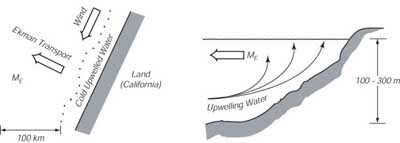
Per vedere come i venti portano all'upwelling, consideriamo i venti da nord che soffiano paralleli alla costa della California (Figura 9.7 sinistra). I venti producono un trasporto di massa via dalla costa dovunque lungo la costa. L'acqua spinta verso il largo può essere rimpiazzata soltanto dall'acqua sotto lo strato di Ekman. Questo è l'upwelling (Figura 9.7 destra). Poiché l'acqua che risale è fredda, il fenomeno porta a regioni con acqua fredda alla superfice lungo la costa. Figura 10.16 mostra la distribuzione di acqua fredda lungo la costa della California.

Figure 9.7 Schema del trasporto di Ekman lungo una costa che produce una risalita di acqua fredda lungo tutta la costa. A sinistra: In sezione. L'acqua trasportata a largo deve essere rimpiazzata dall'acqua che si trova sotto lo strato mescolato. A destra: Dall'alto. Nell'emisfero settentrionale, i venti da nord paralleli alla costa producono un trasporto di Ekman verso il largo.

L'acqua di risalita è normalmente più fredda di quella trovata in superfice, ed inoltre è ricca di nutrienti. I sali nutritivi fertilizzano il fitoplankton nel 'mixed layer', che è mangiato dallo zooplankton, che è mangiato dai piccoli pesci, che sono mangiati da pesci più grandi, e così via. Come risultato, le regioni di upwelling sono le acque produttive, che sostengono le maggiori flotte pescherecce della Terra. Le regioni più importanti sono al largo del Perù, della California, Della Somalia, del Marocco e della Namibia.

Ora possiamo rispondere alla domanda che ci siamo fatti all'inizio del capitolo. Perché il clima di San Francisco è così differente da quello di Norfolk, Virginia? Le figure 4.2 o 9.7 mostrano che il vento lungo le coste della California e dell'Oregon ha una forte componente verso sud. Il vento causa upwelling lungo la costa; che porta acqua fredda vicino la spiaggia. La componente del vento verso la costa porta aria più calda dal mare aperto verso l'acqua più fredda, quest'ultima raffredda l'aria vicina al mare, producendo un sottile strato limite freddo. Come l'aria si raffredda, la nebbia si forma lungo la costa. Alla fine, lo strato di aria fredda è soffiato sopra San Francisco, raffredando la città. L'aria più calda sopra lo strato limite, dovuta alla velocità di discesa della circolazione della cella di Hadley nell'atmosfera (vedi Figura 4.3), inibisce la convezione verticale, e la pioggia è rara. La pioggia si forma soltanto quando le tempeste invernali che vengono verso la costa portano forti convezioni molto alte nell'atmosfera.

Naturalmente anche altri processi influenzano il tempo della California e della Virginia.

1. Il 'mixed layer' oceanico tende ad essere sottile nella parte orientale degli oceani, e l'upwelling può facilmente sollevare acqua fredda.
2. Le currenti lungo il lato orientale degli oceani alle medie latitudini tende a portare acque più fredde da alte latitudini.
3. Lo strato limite nell'atmosfera sopra il mare, quello strato di aria umida sopra il mare, è spessa solo poche centinaia di metri nel pacifico orientale vicino la California. é più di un chilometro vicino l'Asia.

Tutti questi processi sono ribaltati al largo delle coste orientali: portano acque calde vicino le spiagge, spessi strati limite e frequenti piogge convettive. Così il clima di Norfolk è molto differente da quello di San Francisco a causa dell'upwelling e della direzione delle correnti costiere.

Ekman Pumping
La variabilità orizzontale del vento che soffia alla superfice porta alla variabilità dei trasporti di Ekman. Poiché la massa deve essere conservata, la variabilità spaziale dei trasporti deve portare a velocità verticali nella parte alta dello strato di Ekman. Per calcolare questa velocità, prima, integriamo l'equazione di continuità (7.19) nella verticale:

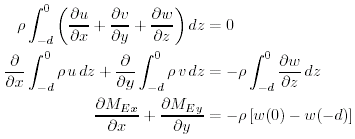	(9.28)

Per definizione, le velocità di Ekman si avvicina a zero alla base dello strato di Ekman, e la velocità verticale alla base dello strato W_E (-d) deve essere zero per la divergenza del flusso di Ekman. Quindi:

	(9.29a)
	(9.29b)

Dove M_E è il vettore del trasporto di massa dovuto al flusso di Ekman nello strato limite superiore dell'oceano, e V_H è l'operatore orizzontale della divergenza e la (9.29) stabilisce che la divergenza orizzontale dei trasporti di Ekman portano ad una velocità verticale nello strato limite superiore dell'oceano, un processo chiamato Ekman Pumping.

Se usiamo il trasporto di massa di Ekman (9.26) nella (9.29) possiamo mettere in relazione l' Ekman pumping con lo sforzo del vento.

	(9.30a)
	(9.30b)

dove T è il vettore dello sforzo del vento.

La velocità verticale alla superfice del mare w(0) deve essere zero perché il livello non può alzarsi verso l'aria, così w_E(0) deve essere bilanciata da un'altra velocità verticale. Vedremo nel Capitolo 12 che è bilanciata dalla velocità geostrofica w_G(0) alla sommità del flusso interno all'oceano.

Da notare che le derivazione riportate sono di Pedlosky (1996: 13), e differiscono dall'approccio tradizionale che porta a velocità verticali alla base dello strato di Ekman. Pedlosky ha sottolineato che lo strato di Ekman è molto sottile comparato alla profondità dell'oceano, non fà differenza se la velocità è calcolata alla cima o al fondo dello strato di Ekman, ma questo è di solito non vero per un oceano. Quindi dobbiamo calcolare la velocità verticale alla cima dello strato.

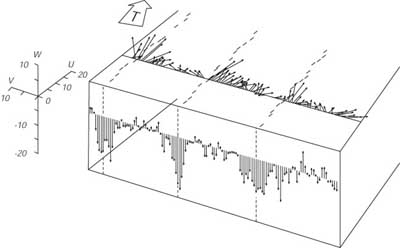
La Circolazione (di) Langmuir
Le misure di corrente di superfice mostrano che il vento genera altre correnti oltre a quelle inerziali e di Ekman. Il vento genera anche una circolazione di Langmuir, una corrente che spiralizza intorno ad un asse parallelo alla direzione del vento. Weller, et al., (1985) hanno osservato tale flusso durante un esperimento per misurare la circolazione forzata dal vento nei primi 50 m del mare. Trovano che durante un periodo di vento con velocità di 14 m/s, le correnti superficiali erano organizzate in celle di Langmuir di 20 m; le celle erano allineate ad un angolo di 15° alla destra del vento; e la velocità verticale a 23 m di profondità erano concentrate in jets stretti sotto le aree di convergenza superficiale (Figura 9.8). La velocità verticale massima era -0.18 m/ s. Il termoclino stagionale era a 50 m, e nessuna velocità verso il basso è stata osservata dentro e sotto il termoclino.

Figura 9.8 Una visione tridimensionale della circolazione di Langmuir osservata dalla piattaforma strumentale gallegiante FLIP, alla superfice del Pacifico. La linea grossa trattegiata indica le linee di convergenza, marcate con strisce alla superfice. Le frecce verticali sono i valori individuali delle velocità verticali misurate ogni 14 secondi a 23m di profondità quando la piattaforma era alla deriva in mezzo alle correnti di Langmuir. Le frecce orizzontali, che sono disegnate alla superfice per chiarezza, sono i valori delle velocità orizzontali a 23m. La grande freccia fornisce la direzione del vento. Da Weller et al. (1985).

9.5 Concetti Importanti

1. I cambiamenti nello sforzo del vento producono oscillazioni transienti nell'Oceano chiamate correnti inerziali.
   (a) Le correnti inerziali sono molto comuni nell'Oceano.
   (b) Il periodo delle correnti è (2π)/f.
   
   
2. I venti stazionari producono un sottile strato limite, lo strato di Ekman, alla cima degli oceani. Gli strati limite di Ekman esistono anche al fondo dell'Oceano ed in atmosfera. Lo strato di Ekman nell'atmosfera sopra la superfice marina è chiamato strato limite planetario.
   
   
3. Lo strato di Ekman alla superfice marina ha le seguenti caratteristiche:
   
   (a) Direzione: 45° a destra del vento guardando sottovento nell'emisfero settentrionale.
   (b) superficiale: 1-2.5% della velocità del vento, dipendente dalla latitudine.
   (c) Profondità: approssimativamente 40-300 m, dipende dalla latitudine e dalla velocità del vento.
   
   
4. Misure accurate della corrente vicino alla superfice marina mostrano che:
   (a) Le oscillazioni inerziali sono la componente più grande nel mixed layer.
   (b) Il flusso e quasi indipendente dalla profondità dentro il 'mixed layer' per periodi vicini a quello inerziale. Così lo strato mescolato si muove orizzontalmente come una piastra con periodo inerziale.
   (c) Uno strato di Ekman esiste nell'atmosfera proprio sopra alla superfice marina (ed alla terraferma).
   (d) Le boe alla deriva sulla superfice marina tendono ad andare parallele alle linee di pressione atmosferica costante. Questo è consistente con la teoria di Ekman.
   (e) Il flusso mediato su molti periodi inerziali è quasi uguale a quello calcolato con la teoria di Ekman.
   
   
5. Il trasporto è a 90° a destra della direzione del vento nell'emisfero settentrionale.
   
   
6. la variabilità spaziale del trasporto di Ekman, dovuto alla variabilità spaziale del vento su distanze di centinaia di chilometri e giorni, porta alla convergenza ed alla divergenza del trasporto.
   (a) I venti che soffiano verso l'equatore lungo le coste occidentali dei continenti producono upwelling. Questo porta ad acque fredde e produttive entro i 100 km dalla costa.
   (b) Acque fatte risalire lungo il fondo occidentale dei continenti modifica il clima lungo le coste occidentali.
   
   
7. La 'Ekman pumping', che è forzata dalla variabilità spaziale dei venti, provoca correnti verticali, che guidano la circolazione geostrofica interna dell'oceano.